Matematické Fórum

lukasstork · 11. 04. 2014 16:04

Ahoj chtěl jsem se zeptat jak zjistíme ze jsou body v jedné přímce diky

Crashatorr · 11. 04. 2014 16:18

Minimální počet bodů, aby to mělo smysl určovat jsou 3 body, protože 2 body vždy leží v jedné přímce. Zjistíš to tak že si vybereš jeden z těch 3 bodů, dejme tomu bod A, pak vypočítáš 2 vektory, oba s počátečním bodem A a koncovým dejme tomu jeden pojmenujeme B a druhý C. Jestli je vektor AB násobkem vektoru AC, pak všechny 3 body leží v jedné přímce, pakliže vektor AB není násobkem vektoru AC pak neleží na jedné přímce

Honzc · 13. 04. 2014 08:48 — Editoval Honzc (13. 04. 2014 08:51)

↑ lukasstork:
Aby 3 body 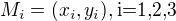$M_{i}=(x_{i},y_{i}),\text{i=1,2,3}$ ležely v jedné přímce stačí, aby determinant
$D=\begin{vmatrix} x_{1} & y_{1} & 1\\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{vmatrix}=0$
Navíc pokud zjistíš,že determinant není roven nule, pak jeho absolutní hodnota podělená číslem 2 udává obsah trojúhelníka sestrojeného z těchto 3 bodů.

Matematické Fórum

#1 11. 04. 2014 16:04

body v jedné primce

#2 11. 04. 2014 16:18

Re: body v jedné primce

#3 13. 04. 2014 08:48 — Editoval Honzc (13. 04. 2014 08:51)

Re: body v jedné primce

Zápatí