Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 04. 2014 19:57
goniometricke rovnice
Ahoj, chtěl bych se zeptat na tento příklad. Správná odpověď je 3 řešení. Jenže já v intervalu pi do 2pi tedy (od 3. do 4. kvadrantu) vidím dvě řešení, kde je to 3.? Předem díky.
Počet všech  , pro která platí:
, pro která platí:  , je roven číslu:
, je roven číslu:
a) 3 b) 2 c) 4 d) 1

1.

2.




Offline
- (téma jako vyřešené označil(a) bonifax)
#2 15. 04. 2014 20:03
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: goniometricke rovnice
Však na tom obrázku máš vyznačeny tři řešení, tři kořeny, tři různá x:) 1 kořen získáš z rovnice cosx=0 a další dvě z rovnice sinx=-1/2. Sinus nabývá záporných hodnot ve 3. a 4,. kvadrantu a cosx=0 ve 3. nebo 4. kvadrantu má taky řešení:)
Offline


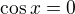
 Nikoliv 2kpi.
Nikoliv 2kpi.
 a
a 