Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 04. 2014 05:57
Pravděpodobnost
Určete součet ok, který při hodu třemi kostkami padne nejčastěji.
Výsledek by měl být: nejpravděpodobnější jsou součty 10 a 11 ( oba tutéž 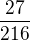 )
)
Zaboha se k té 27 nemůžu dohrabat, tak jestli bych Vás mohl požádat zase o menší nakopnutí, bylo by to super.
Offline
#4 19. 09. 2025 20:53 — Editoval JuraPopu (26. 09. 2025 03:48)
Re: Pravděpodobnost
Intuitivní úvaha pro n kostek, Edit: kdy pro n předpokládáme aspoň 2 kostky (fakt jen intuitivní, třeba se mýlím, kvalitní úvahy nechávám na kovaných kombinatorikomilech):
Pro sudá n vždycky jeden součet 3,5n (vyjde přir. číslo, paráda).
Pro lichá n vždycky 2 součty, a sice 3,5n-0,5 a 3,5n+0,5
3,5 je (mělo by být) průměrný číslo, co padne při hodu jednou (poctivou) kostkou.
Může být?
Offline
#5 19. 09. 2025 22:14
#7 21. 09. 2025 10:59
Re: Pravděpodobnost
↑ JuraPopu:
Keď sem niekto zadá úlohu, očakáva odpoveď (na to je fórum určené).
Po cca 10 rokoch autor sotva príde odpoveď prečítať.
A tie tisícročia vari nemyslíš vážne - či?
Btw - máš pocit, že si odpovedal na otázku zadávateľa?
Offline
#8 21. 09. 2025 15:59 — Editoval JuraPopu (21. 09. 2025 16:00)
Re: Pravděpodobnost
Nahořejc vidno, že jsem položil navazující, související otázku, na čemž nevidím nic špatnýho.
Dovolím si nadále nevěřit, že úloha úplně nahoře vznikla až v roce 2014 (tj. že je "úloha z roku 2014"):
https://cs.wikipedia.org/wiki/Hrac%C3%AD_kostka
Ale dobrá, záleží na tom, co si kdo představuje pod rčením "úloha z roku 2014".
Tím to pro mě hasne, nepíšu sem kvůli hádkám, fakt ne.
Spíš jsem tady čekal nějakou zajímavou úvahu (na téma matematika).
Offline
#9 22. 09. 2025 16:50
#10 22. 09. 2025 19:45
#11 22. 09. 2025 19:58 — Editoval JuraPopu (22. 09. 2025 20:03)
Re: Pravděpodobnost
Ahoj, no, když se ptáme na součet, tak k tomu potřebujem aspoň 2 počty ok, tj. na 2 kostkách. Aspoň tak tomu rozumím já osobně.
Mám to editovat a připsat, že to myslím pro
[mathjax]n\ge 2[/mathjax]
???
PS: Ale jinak má intuitivní rychlokvaška pravdu, jest tak?
Offline
#12 23. 09. 2025 11:11
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Pravděpodobnost
↑ JuraPopu:
Připadá mi to pravděpodobné, ale muselo by se to dokázat.
PS: Někdy se i jedno číslo považuje za součet, to záleží na konkrétním problému.
"Máte úhel beta." "No to nemám."
Offline
