Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 04. 2014 14:11 — Editoval alofokolo (17. 04. 2014 14:51)
Úloha na geometrii
Dobrý den, dívám se na některé úlohy z klokana, a s některými si nevím rady. Například tady, s úlohou 17.
Zkusil jsem si za strany obdélníku dosadit vlastní neznámé (za delší 16, za kratší 12) - tak se úsečky mezi středy stran rovnaly 10 cm. Tohle, mi ale moc nepomohlo - nevím, jak se dostat k výsledku. Poradíte prosím?
Offline
- (téma jako vyřešené označil(a) alofokolo)
#3 17. 04. 2014 14:59 — Editoval Freedy (17. 04. 2014 19:22)
Re: Úloha na geometrii
Ahoj,
označme si:![kopírovat do textarea $A [0;0]$](/mathtex/7d/7ddfe607ae34b449a8abf7cfdf001694.gif)
![kopírovat do textarea $B [a;0]$](/mathtex/30/309f470f83f89467a0ff87f95e543af4.gif)
![kopírovat do textarea $C [a;b]$](/mathtex/08/080db82a69b0ec27924e66fe1e7a0111.gif)
![kopírovat do textarea $D [0;b]$](/mathtex/d8/d874d4535461630d0b3738e36d933013.gif)
středy stran jsou potom:![kopírovat do textarea $S_{AB} = P = [\frac{a}{2};0]$](/mathtex/42/42a10326f865d6e90840d05a8bfc3f3d.gif)
![kopírovat do textarea $S_{BC} = Q =[a;\frac{b}{2}]$](/mathtex/49/49893d4d996d82d810b574720541e151.gif)
![kopírovat do textarea $S_{CD} = R =[\frac{a}{2};b]$](/mathtex/63/639893fa4dd45ef2729e1590a4fd3e84.gif)
![kopírovat do textarea $S_{AD} = S =[0;\frac{b}{2}]$](/mathtex/62/6294ef1de2853f9d7dd1b9b8c5046773.gif)
Střed úsečky RS![kopírovat do textarea $S_{RS}=T=[\frac{a}{4};\frac{3b}{4}]$](/mathtex/21/2139a867e0e7d95ae0c23c67ff75655c.gif)
Můžeme určit obsah trojúhelníku PQT pomocí vektorového součinu jeho dvou vektorů: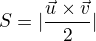
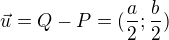

Obsah trojúhelníku tedy je: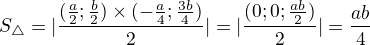
Obsah obdelníku je pochopitelně 
Poměr těchto obsahů:
PS: analytickou geometrií jde všechno
EDIT: díky vanok, opraveno
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 17. 04. 2014 15:04 — Editoval xstudentíkx (17. 04. 2014 16:33)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Úloha na geometrii
Ahoj ↑ alofokolo:
Trochu jsem se na to podívala a napadá mě toto řešení:
Přidávám i obrázek, aby jsi to v tom lépe viděl:
Delší strana má 84 , kratší 56 (2/3 delší).
Vidíš tam 2 pravoúhlé trojúhelníky, které jsou stejně velké a jsou rozdělené v 1/3 dané strany, proto lze snadno vypočítat jejich obsah (18,666...*42= 784, aby jsi získal obsah, musíš to vydělit dvěma, ale jelikož je druhý stejný, tak ani nemá cenu to rozdělovat, můžeš si to sám ověřit).
Pak máme tu největší část trojúhelníka (PQ a střed), která má obsah (28*42)/2, což je 588.
Když toto sečteme, 784+588 = 1372 a obsah celého obdélníku je 4704, z toho je 1176 čtvrtina, náš výsledek je vyšší a to v něm není započítaná "špička", tudíž je zřejmé, že to musí být 5/16, nebo-li odpověď A
Toto je moje řešení, sice není úplné, ale k výsledku stačí. Je to spíše jednodušší postup, a proto se můžu mýlit.
Offline
#8 17. 04. 2014 15:43
Re: Úloha na geometrii
V danom pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C označme D pätu výšky z vrcholu C. Nech X je lubovoµný vnútorný bod úsečky CD. Označme K taký bod na úsečke AX, že |BK| = |BC|. Podobne označme L taký bod na úsečke BX, že |AL| = |AC|. Priesečník priamok AL a BK označme M. Dokážte, že |MK| = |ML|.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 17. 04. 2014 15:46 — Editoval BakyX (17. 04. 2014 15:47)
Re: Úloha na geometrii
↑ Freedy:
http://skmo.sk/dokument.php?id=408
Úloha 6
Alebo toto :)
Given is a quadrilateral ABCD in which we can inscribe circle. The segments AB, BC, CD and DA are the diameters of the circles o1, o2, o3 and o4, respectively. Prove that there exists a circle tangent to all of the circles o1, o2, o3 and o4.
Je toho 1000...
1^6 - 2^6 + 3^6 = 666
Offline
#10 17. 04. 2014 16:51
Re: Úloha na geometrii
Daný je ostroúhlý trojúhelník ABC a kružnice k jemu opsaná. Nechť l je tečna kružnice k a l_a, l_b, l_c jsou obrazy přímky l v osových souměrnostech podle přímek BC CA AB. Dokažte že kružnice opsaná trojúhelníku určenému přímkami l_a, l_b, l_c se dotýká kružnice k.
Začneme volbou bodů:![kopírovat do textarea $A [0;0]$](/mathtex/7d/7ddfe607ae34b449a8abf7cfdf001694.gif)
![kopírovat do textarea $B[a;0]$](/mathtex/90/90a4e9f780736b66df10b2237e656dc0.gif)
![kopírovat do textarea $C[b;c]$](/mathtex/17/17314b3d68f6c63cfe193af5e0dcfb1a.gif) kde platí:
kde platí:  (musí být ostroúhlý)
(musí být ostroúhlý)
Kružnice procházející těmito body se dá pomocí 3 bodů zjistit snadno: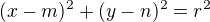
dosadíme bod A a máme:
dosadíme bod B a máme:
dosadíme bod C a máme: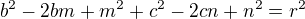
řešením těchto tří rovnic zjistíme: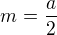
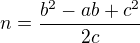
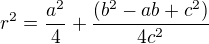
Máme tedy rovnici kružnice opsané trojúhelníku ABC: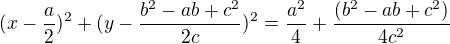
Tečna v bodě [x0;y0] má rovnici: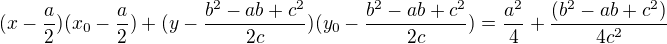
Po menších úpravách můžeme tuto rovnici upravit na tvar: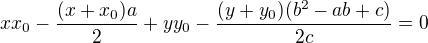
Nyní je potřeba udělat obrazy této přímky podle přímek AB BC AC.
Tak a nyní už by to bylo tak pracný udělat ty obrazy, že bych se do toho pustil pouze s nějakou motivací. Vyplivlo by to směsici písmen a čísel, která by na konci ukázala, že pro a,b,c z R kde 0< b < a vychází právě jeden průsečík těch dvou kružnic
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#11 17. 04. 2014 19:12 — Editoval vanok (17. 04. 2014 19:14)
Re: Úloha na geometrii
ahoj ↑ Freedy:,
Analytika je mocny nastroj, ale je citlivy na chyby.
Tak skontroluj tvoje vypocty.
Toto napr. 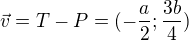
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 17. 04. 2014 19:17
- Eratosthenes
- Příspěvky: 2584
- Reputace: 132
Re: Úloha na geometrii
↑ Freedy:
Ahoj,
poněkud mi uniká, co má tvůj příklad společného se zadanou úlohou...
Budoucnost patří aluminiu.
Offline
#13 17. 04. 2014 19:18 Příspěvek uživatele Freedy byl skryt uživatelem Freedy.
#14 17. 04. 2014 19:24
Re: Úloha na geometrii
Poznamka: spravna odpoved je ↑ byk7:.
Inac jedna rychla metoda dokazu je: nech U je stred usecky PQ.
Potom sa lahko dokaze ze obsah PQT, je rovny obsahu PUTS a ten je 1/4 obsahu odlznika.
Inac velmi rychly dokaz, pre znalcov geometrie, sa mohol urobit aj na stvorci strany 1( napr.) Preco?
Kde sa najdu texty tychto zabavnych cviceni?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 17. 04. 2014 19:29
Re: Úloha na geometrii
↑ Freedy:
Tvoja metoda prace je Ok.
Az na tu chybu, lebo asi si chcel ist rychlo.
A pozor, v tvojom vektorovom sucine musis pouzit 3 dim. na vsetki vektory.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 18. 04. 2014 07:21 — Editoval Honzc (18. 04. 2014 07:28)
Re: Úloha na geometrii
↑ alofokolo:
I když řešení podle ↑ byk7: je velice elegantní, tak také přispěji:
Z obrázku
je zřejmé, že požadovaná plocha je rozdílem plochy obdélníka a součtu 4 trojúhelníků a dvou lichoběžníků, přičemž vždy 2 (černé šrafování) a 2 (červené šrafování) trojúhelníky mají stejný obsah a taktéž oba (modré šrafování) lichoběžníky mají stejný obsah.
Protože chceme znát poměr ploch a všechny plochy obsahují součin 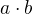 a také plocha původního obdélníku je
a také plocha původního obdélníku je 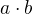 stačí spočítat:
stačí spočítat: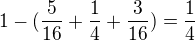 a to je i výsledek.
a to je i výsledek.
Offline
#18 18. 04. 2014 10:47
Re: Úloha na geometrii
Zdravím, v kategoriích Junior (1.+2.r.) a Student (3.+4.r. středních škol) je ba vyřešení 24 úloh vyhrazen časový limit 75 min. Proto i když jsou řešení Freedyho a Honzce/Cheopa správná, jsou příliš časově náročná.
↑ vanok: Např. zde.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
