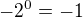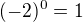Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 04. 2014 09:57
#3 19. 04. 2014 10:35
Re: Cokoliv na nultou
Ahoj,
uvažujme: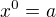 pro
pro 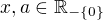
Nula je zajímavé číslo v tom, že jako pro jediné platí: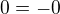
Díky tomuto faktu je možné tvrdit že: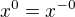
Stačí pravou stranu upravit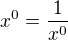 a následně
a následně 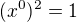
Použitím pravidel o umocňování je to vlastně 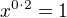 >>>
>>> 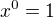 . Pokud tedy umocňujeme jakékoliv číslo různé od nuly na nultou, výsledkem bude vždy 1.
. Pokud tedy umocňujeme jakékoliv číslo různé od nuly na nultou, výsledkem bude vždy 1.
Jiné vysvětlení lze vidět i v příkladu že: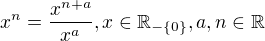
Pokud by tedy bylo n = 0, a jakékoliv reálné číslo, tak dostáváme: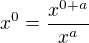
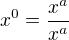
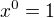
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline