Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 04. 2014 16:30
Eulerova identita
Zdravím, potřeboval bych trochu poradit s eulerovou identitou a komplexními čísly obecně.
Vím, že 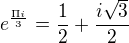 , ale jak bych si tohle mohl sám odvodit, popřípadě i pro jiné hodnoty jmenovatele?
, ale jak bych si tohle mohl sám odvodit, popřípadě i pro jiné hodnoty jmenovatele?
Vím taky že se to přepsat jako ![kopírovat do textarea $\sqrt[3]{-1}$](/mathtex/82/82c0f4e55e47399451704f6793fa9555.gif) . Intuice mi říká, že výsledek téhle odmocniny je -1, ale není to tak.
. Intuice mi říká, že výsledek téhle odmocniny je -1, ale není to tak.
Předem díky za odpověď.
Offline
- (téma jako vyřešené označil(a) Akcope)
#2 19. 04. 2014 16:42
Re: Eulerova identita
Stačí využít toho že:
Dále nemůžeš v tom zlomku v čitateli chápat odmocninu. Už jen z toho důvodu že 3. odmocnina z mínus jedničky má 3 komplexní kořeny (z toho jeden je reálný)
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
