Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 25. 04. 2014 17:07

Crashatorr
Příspěvky: 360
Reputace:   7 
 

Kružnice vepsaná trojúhelníku- analyticky

Zdravím,
Narazil jsem na jeden příklad, který už se tady řešil, ale ne nějak podrobněji:
Napište rovnici kružnice vepsané trojúhelníku KLM, je-li K[2,1], L[6,4], M[6,1].
Pomocí náčrtku a pár výpočtů jsou schopen tu rovnici zjistit docela jednoduše, ale zajímalo by mě jestli se to dá vypočítat čistě analytickým přístupem, aniž bych si musel cokoliv kreslit. Rozhodně mi přijde jednodušší nakreslit si to a dopočíst, ale chci znát i ostatní způsoby.
Díky předem za všechny rady:)

Offline

  • (téma jako vyřešené označil(a) Crashatorr)

#2 25. 04. 2014 17:13

Jj
Příspěvky: 8767
Škola: VŠB, absolv. r. 1970
Pozice: Důchodce
Reputace:   599 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ Crashatorr:

Dobrý den, řekl bych, že třeba hledat průsečík tří os úhlů trojúhelníka, hledat bod stejně vzdálený od tří stran trojúhelníka.

Pokud se tedy nemýlím.

Offline

 

#3 25. 04. 2014 17:17

BakyX
Cat Lover & S.O.A.D. Lover
Příspěvky: 3416
Škola: UPJŠ
Pozice: Študent
Reputace:   158 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ Jj:

Šlo by aj napísať rovnice osí uhlov. Stačí 2.

1^6 - 2^6 + 3^6 = 666

Offline

 

#4 25. 04. 2014 17:22

Crashatorr
Příspěvky: 360
Reputace:   7 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ Jj:
Vím že vzdálenost od přímky KL 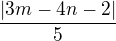$\frac{|3m-4n-2|}{5}$
od KM 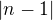$|n-1|$
od ML 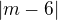$|m-6|$

Jestli mám brát v potaz i ty absolutní hodnoty tak to vypadá na dýl:) Co bych s tím měl dělat teďka?

Offline

 

#5 25. 04. 2014 18:09

BakyX
Cat Lover & S.O.A.D. Lover
Příspěvky: 3416
Škola: UPJŠ
Pozice: Študent
Reputace:   158 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ Crashatorr:

Úprimne si nemyslím, že je to najlepšia cesta, lebo toto má 4 riešenia. Radšej skús tie osy.

1^6 - 2^6 + 3^6 = 666

Offline

 

#6 25. 04. 2014 18:13

Jj
Příspěvky: 8767
Škola: VŠB, absolv. r. 1970
Pozice: Důchodce
Reputace:   599 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ Crashatorr:

Nevím, jak to úsporně řešit. A v případné obecné poloze přímek teprve ne.

Pokud se tedy nemýlím.

Offline

 

#7 25. 04. 2014 18:13

Crashatorr
Příspěvky: 360
Reputace:   7 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ BakyX:
Směrové vektory těch os zjistím pomocí vekorového součtu? oplněním na rovnoběžník ?

Offline

 

#8 25. 04. 2014 18:16

BakyX
Cat Lover & S.O.A.D. Lover
Příspěvky: 3416
Škola: UPJŠ
Pozice: Študent
Reputace:   158 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ Crashatorr:

No áno. Vezmeš rovnako dlhé vektory v smere požadovaných polpriamok tvoriacich uhol, sčítaš ich. Ich súčet má smer osy uhla tvorenej tými polpriamkami.

1^6 - 2^6 + 3^6 = 666

Offline

 

#9 25. 04. 2014 18:20

Crashatorr
Příspěvky: 360
Reputace:   7 
 

Re: Kružnice vepsaná trojúhelníku- analyticky

↑ BakyX:
Chytré:) zbytek už zvládnu dopočítat, děkuju za pomoc

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson