Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 26. 04. 2014 11:19 — Editoval vanok (26. 04. 2014 11:23)
Re: Rovnice s parametrem
Ahoj ↑ Kaki:,
Skor zacni takto:
Po uprave tvoja rovnica da  ,
,
To da pre  , cize pre
, cize pre 

Ze to uz vies ukoncit.
Poznamka: tvoje podmienky si napisala priliz skoro, tie sa tykaju len hodnot p, pre ktore sa neda vypocitat po upravach x.... A potom pre tie hodnoty p, sa vrati do povodnej rovnice a sa to specialne prestuduje.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 26. 04. 2014 11:21
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Rovnice s parametrem
↑ Kaki:
Ahoj,
Řekl bych, že to není dobře. Obě závorky nejdřív roznásob a pak teprve urči, pro které p je rovnice lineární:)
Offline
#6 26. 04. 2014 13:31
#9 27. 04. 2014 22:14
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Rovnice s parametrem
↑ marnes:
Myslím že je třeba brát upravený tvar. Lineární rovnice má tvat y=ax+b, takže podle mého názoru nemůžeš brát takový tvar a rozhodovat o tom jestli je nebo není lineární, navíc po úpravách dojdeme ke tvaru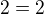 resp
resp 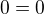 , což lze těžko posuzovat jako lineární rovnici. Rád si poslechnu názory ostatních:)
, což lze těžko posuzovat jako lineární rovnici. Rád si poslechnu názory ostatních:)
Offline
#10 27. 04. 2014 22:21
- marnes

- Příspěvky: 11195
Re: Rovnice s parametrem
↑ Crashatorr:
Názor ostatních také rád vyslechnu.
Rovnici 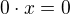 za lineární považuji a má nekonečně mnoho řešení
za lineární považuji a má nekonečně mnoho řešení
Jo. A na začátku vás zdravím.
Offline
#11 27. 04. 2014 22:25
Re: Rovnice s parametrem
Pozdravujem ↑ marnes:,
Ja to vidim takto:
Rozhodnut o tom, ci ide o linearnu rovnicu, alebo nie sa da rozhodnut len po napisani do tvaru a.x= b
Ak a je nenulove tak ide o lin. rovnicu.
Inac nejde o lin. rovnicu.
Ak a=0, a b=0, 0.x=0 je pravdivy vyrok, co znamena, ze kazde realne x, vyhovuje relacii 0.x=0.
Ak a=0, b nenulove mame nepravdivy vyrok ....
( no ako casto je to otazka dohody)
Aku ty pouzivas?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 27. 04. 2014 22:25
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Re: Rovnice s parametrem
↑ marnes:
Řekl bych že pak záleží na definici lineární rovnice. U nás na škole se učí tak, že y=ax+b, kde a je různé od nuly. Jestli bereš lineární rovnici y=ax+b pro všechna a tak v tom případě je lineární, asi na tom moc nesejde, řešení té rovnice je jasné a o jedinou správnou terminologii se můžeme hádat kdo ví jak dlouho:)
Offline
#13 28. 04. 2014 00:18 — Editoval Freedy (28. 04. 2014 00:33)
Re: Rovnice s parametrem
marnes napsal(a):
Rovnici
za lineární považuji a má nekonečně mnoho řešení
Zdravím, dobrá, můžeme teda ale předpokládat, že lineární rovnice má:
jedno řešení v případě:
žádné řešení v případě: - v tuto chvíli se jedná o nepravdivý výrok, to je to samé jako tvrdit 5 = 17.
- v tuto chvíli se jedná o nepravdivý výrok, to je to samé jako tvrdit 5 = 17.
nekonečně mnoho řešení v případě: - zde se zase jedná o pravdivý výrok, to ten že 6 = 6 například. (6+ 0x = 6 >> 0x = 0)
- zde se zase jedná o pravdivý výrok, to ten že 6 = 6 například. (6+ 0x = 6 >> 0x = 0)
Podle mě definice:
Lineární rovnice lze upravit na tvar  kde
kde 
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline



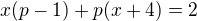

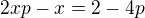

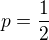 >>>
>>> 
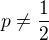 >>>
>>>