Matematické Fórum

Smulis · 29. 04. 2014 22:21

Dobrý den, nedávno jsem narazil na rovnici, kterou jsem nedokázal vyřešit: $2^{x} = 3x$

Rovnici jsem zkoušel zadat i do Geogebry, ale ta si s tím také neví rady. Ke kořenům jsem se nakonec dostal grafickým řešením v Geogebře. (zadal jsem zvlášť levou a pravou funkci a zjistil jejich průsečíky) Kořeny jsou podle všeho dva a to: 0.45782... a 3.31318...

Snažil jsem se najít nějaké řešení na internetu a našel jsem pouze tohle: http://www1.math.american.edu/People/ka … s/glog.pdf

To, že je článek v angličtině mi až takový problém nedělá, ale obávám se, že bych mu nerozumněl ani v češtině. Jestli je někdo ochotný mi nastínit řešení, byl bych vděčný. Děkuji.

runcorne

No, nijak jsem to nestudoval..., ale píší tam...:

„But in terms of the elementary functions of calculus
and college algebra, there is no analytic solution.“

Což bych chápal tak, že standartními postupy nelze získat analytické řešení... a lze to vyřešit jen numericky.

A ve zbytku článku zavádí autor jakousi funkci glog, přes kterou by to možná mělo jít. (?) Ale tohle nevím jistě, nečetl jsem to, zítra se na to podívám...., a snad se tam nějaká možnost řešení najde...

Freedy · 29. 04. 2014 23:34

Ahoj,

tomu postupu v článku také moc nerozumím.
Pokusím se ti nastínit metodu řešení nelineárních rovnic newtonovou metodou:
Tato metoda spočívá v tom, odhadnout přibližné řešení a pomocí metody tečen se k němu "přibližovat" a aproximovat ho na co nejpřesnější hodnotu.
Je potřeba si představit ty dva grafy a nebo jednoduše odzkoušet pár hodnot a zjistit kde se "protínají"
x = -1 >>> 0,5 = -3
x = 0 >>> 1 = 0
x = 1 >>> 2 = 3
x = 2 >>> 4 = 6
x = 3 >>> 8 = 9
x = 4 >>> 16 = 12

můžeme si všimnout že levá strana je větší v 0 než pravá ale v 1 už je menší než pravá. Proto mezi 0 a 1 bude pravděpodobně kořen
Dále v 3 je hodnota levé strany menší než hodnota pravé ale ve 4 už je levá strana větší než pravá, proto mezi 3 a 4 bude další kořen. Další kořeny nejsou možné.

Budeme teda hledat řešení v blízkosti x = 1/2 a x = 7/2.

Metoda spočívá v tomto vzorci: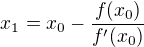
$x_1=x_0-\frac{f(x_0)}{f'(x_0)}$

hledáme nulové body funkce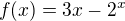
$f(x) = 3x - 2^x$
derivace dané funkce: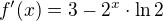
$f'(x) = 3 - 2^x\cdot\ln 2$

kořen x = 1/2

1. iterace: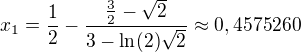
$x_1=\frac{1}{2}-\frac{\frac{3}{2}-\sqrt{2}}{3-\ln (2)\sqrt{2}}\approx 0,4575260$
2. iterace: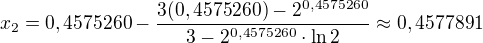
$x_2=0,4575260-\frac{3(0,4575260) - 2^{0,4575260}}{3-2^{0,4575260}\cdot\ln 2}\approx 0,4577891$
posunuli jsme se o 2 tisíciny nahoru. Pokud bychom pokračovali, pořád bychom se blížili blíž a blíž hledanému kořenu.

kořen x = 7/2
1. iterace:
$x_1=\frac{7}{2}-\frac{\frac{21}{2}-\sqrt{2^7}}{3-\ln 2\sqrt{2^7}}\approx 3,331950113400$
2. iterace: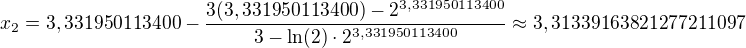
$x_2=3,331950113400-\frac{3(3,331950113400)-2^{3,331950113400}}{3-\ln (2)\cdot2^{3,331950113400}}\approx 3,31339163821277211097$
zde už je posun větší a to o 2 setiny, proto zkusíme 3 iteraci
3. iterace:
$x_3=3,31339163821277211097 - \frac{3(3,31339163821277211097) - 2^{3,31339163821277211097}}{3-2^{3,31339163821277211097}\cdot\ln 2}\approx 3,31317840838983100585422$

zde už se ta hodnota liší fakt minimálně, konkrétně o nějaké 2 tisíciny.
Iterací můžeš dělat kolik chceš a pokud by jsi iteroval do nekonečna, dostal by jsi se na přesnou hodnotu.
Tady pouze záleží na tom, na kolik desitinných míst chceš mít tu hodnotu přesnou.

Eratosthenes · 29. 04. 2014 23:35

ahoj ↑ Smulis:,

většinu rovnic nelze řešit přímo (tj. neexistuje nějaký vzoreček, do kterého dosadíš a máš kořeny), ale je třeba je řešit numericky (ta tvoje je jednou z nich). Numerické metody sice po konečném počtu kroků nedají teoreticky přesný výsledek, ale dají výsledek s předem požadovanou přesností. Takových metod je celá řada, i literatury a webových pramenů kolem nich jsou tuny. Zkus třeba:

http://cmp.felk.cvut.cz/~navara/nm/koreny.pdf

nebo

http://mathonline.fme.vutbr.cz/Reseni-n … fault.aspx

Smulis · 30. 04. 2014 21:26

Ahoj ↑ Freedy:↑ Eratosthenes:

Obě odpovědi mi hodně pomohly. A dokonce mi odpověděly na některé další typy rovnic. Díky. :-)

Matematické Fórum

#1 29. 04. 2014 22:21

exponenciální-lineární rovnice

#2 29. 04. 2014 23:26 — Editoval runcorne (29. 04. 2014 23:31)

Re: exponenciální-lineární rovnice

#3 29. 04. 2014 23:34

Re: exponenciální-lineární rovnice

#4 29. 04. 2014 23:35

Re: exponenciální-lineární rovnice

#5 30. 04. 2014 21:26

Re: exponenciální-lineární rovnice

Zápatí