Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určitý integrál - dlžka krivky (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 05. 2014 11:43
Určitý integrál - dlžka krivky
Zdravím. Mám problém s vyrátaním určitého integrálu pri výpočte dlžky krivky. Dostanem integral v tvare 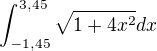 . Neviem ako si poradiť s tou odmocninou. Vie mi niekto pomôcť, prosím ? Ďakujem
. Neviem ako si poradiť s tou odmocninou. Vie mi niekto pomôcť, prosím ? Ďakujem
Offline
- (téma jako vyřešené označil(a) jelena)
#2 01. 05. 2014 12:02
Re: Určitý integrál - dlžka krivky
Ahoj,
tento příklad je jako dělaný na substituci. Můžeš vyzkoušet například:
1) 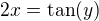
2) 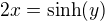
3) 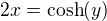
Integrál pak přejde na snadnější formu, kterou by už neměl být problém vypočítat.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 01. 05. 2014 15:00
Re: Určitý integrál - dlžka krivky
Ahoj,
tak třeba substituce: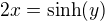
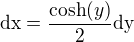
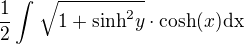
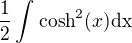
Tento integrál vypadá poměrně pěkně, abychom ho vyřešili, musíme vyjít z definice této hyperbolické funkce: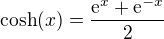
Máme tedy integrál: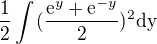
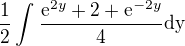
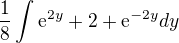
Toto už je velice jednoduché integrovat: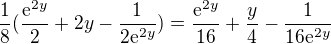
Máme tedy: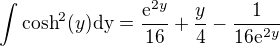
Na začátku byla použita substituce: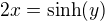
Vyjádříme y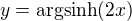
A dosadíme: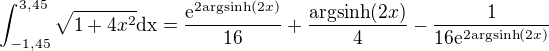
Vypadá to možná hrůzostrašně.
Pokud ale využiješ tohoto faktu: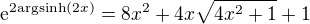
Lze výsledek upravit: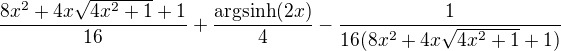
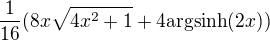
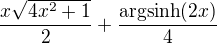
Zde už se s tím nic víc vyrobit nedá. Proto už jen zbývá dosadit a zmáčknout na kalkulačce.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 01. 05. 2014 15:29 — Editoval Jj (01. 05. 2014 15:34)
Re: Určitý integrál - dlžka krivky
↑ Freedy:
Zdravím, řekl bych, že substituce je správná, ale postup se dá podstatně zkrátit:
Podobně jako u goniometrických, tak i u hyperbolických funkcí platí identita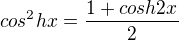 .
.
Takže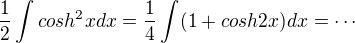
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určitý integrál - dlžka krivky (TOTO TÉMA JE VYŘEŠENÉ)
