Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 05. 2014 12:09 — Editoval janca361 (02. 05. 2014 13:38)
- janca361

- .
- Příspěvky: 3284
Řešení maturitního testu jaro 2014
Zdravím,
řešení maturitního testu z 2.5.2014.
Zadání: Odkaz
Výsledky jsou bez záruky. Objevíte-li chybu, upozorněte na ni prosím.
Stejně tak každý může přidat řešení - nejen výsledek, ale i postup!
Své dojmy a pocity (mimo výpočtů a dotazů na úlohy) můžete sdílet zde.
Videořešení maturity z projektu Matika mailem: Odkaz (kliknutím na jednotlivá zadání se zobrazí dané video)
Offline
#2 02. 05. 2014 12:10 — Editoval janca361 (02. 05. 2014 13:11)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
1.
Řešení:
Obsah obdélníčku je: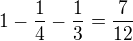
Zbývá tedy 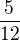 obdélníku a tmavá plocha je polovinou
obdélníku a tmavá plocha je polovinou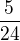
Za řešení děkuji kolegovi marnes.
Jiný postup řešení:
Offline
#4 02. 05. 2014 12:13 — Editoval marnes (02. 05. 2014 12:21) Příspěvek uživatele marnes byl skryt uživatelem janca361. Důvod: Doplněno k danému zadání. Děkuji!
#6 02. 05. 2014 12:15 — Editoval janca361 (02. 05. 2014 12:20)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
4.
Řešení: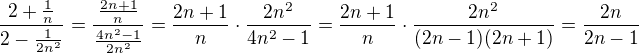
Pozn: Žádná podmínka není potřeba, jelikož 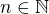 .
.
Offline
#7 02. 05. 2014 12:16 — Editoval janca361 (02. 05. 2014 13:13)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
5.
Řešení:
Podmínky: 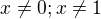
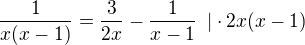


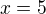
Děkuji gadgetko!
Offline
#8 02. 05. 2014 12:20 Příspěvek uživatele gadgetka byl skryt uživatelem janca361. Důvod: Doplněno k danému zadání. Děkuji!
#10 02. 05. 2014 12:24
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
7.
Řešení:
Obor hodnot funkce sinus je  . Nás zajímá v kterém bodě (pro jaké
. Nás zajímá v kterém bodě (pro jaké  ) je hodnota funkce -1.
) je hodnota funkce -1.
Pozor! Není možné zapsat jako 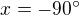 , protože toto číslo neleží v definičním oboru!
, protože toto číslo neleží v definičním oboru!
Offline
#11 02. 05. 2014 12:25 — Editoval gadgetka (02. 05. 2014 12:25) Příspěvek uživatele gadgetka byl skryt uživatelem janca361. Důvod: Doplněno k danému zadání. Děkuji!
#12 02. 05. 2014 12:27 — Editoval byk7 (03. 05. 2014 14:44)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
8.
Řešení:
8.1
Grafem je parabola otočená směrem dolů s vrcholem v bodě V[0;4]
8.2
Pro průsečík s osou y platí:  - průsečíkem je tedy vrchol paraboly -
- průsečíkem je tedy vrchol paraboly - ![kopírovat do textarea $P[0;4]$](/mathtex/bc/bc702015e0bb078214abb4ebbdd35c1e.gif)
8.3
Offline
#14 02. 05. 2014 12:29 — Editoval zdenek1 (02. 05. 2014 12:36)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
10.
Jelikož má čtverec obsah 400 cm^2, je délka jeho strany 20 cm.
Čtyři obarvené čtvrtkruhy tvoří kruh s poloměrem 10 cm.
Jeho obsah je 
Offline
#15 02. 05. 2014 12:31 — Editoval janca361 (02. 05. 2014 12:38)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
11.
Řešení:
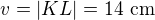
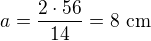
Díky Crashatorr za opravu!
Offline
#16 02. 05. 2014 12:34 Příspěvek uživatele Crashatorr byl skryt uživatelem janca361. Důvod: Díky, opraveno.
#17 02. 05. 2014 12:37
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
12.
Řešení:
Vzdálenost je 4 cm (viz obrázek).
Offline
#18 02. 05. 2014 12:38 — Editoval gadgetka (02. 05. 2014 12:39) Příspěvek uživatele gadgetka byl skryt uživatelem janca361. Důvod: Doplněno k danému zadání. Děkuji!
#19 02. 05. 2014 12:42 Příspěvek uživatele janca361 byl skryt uživatelem janca361. Důvod: Máš pravdu ;)
#20 02. 05. 2014 12:43 Příspěvek uživatele gadgetka byl skryt uživatelem janca361. Důvod: OK.
#21 02. 05. 2014 12:45 Příspěvek uživatele Crashatorr byl skryt uživatelem janca361. Důvod: Máš pravdu ;)
#23 02. 05. 2014 12:48 — Editoval janca361 (02. 05. 2014 13:14)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
14.
Řešení:
Rychlost Petra je 
Rychlost Martina je 
Pokud Petr sám pracuje čas  , musí platit rovnice
, musí platit rovnice

Díky zdenku za řešení!
Offline
#24 02. 05. 2014 12:49 — Editoval zdenek1 (02. 05. 2014 13:34)
- janca361

- .
- Příspěvky: 3284
Re: Řešení maturitního testu jaro 2014
15.
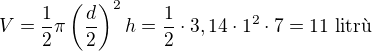
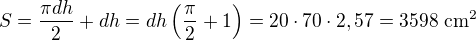
pokud se počítá  s předdefinovanou hodnotou na kalkulačce, vychází 3599 cm^2
s předdefinovanou hodnotou na kalkulačce, vychází 3599 cm^2
Offline
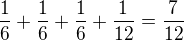
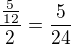



![kopírovat do textarea $3[a-a(a-1)]^{2}=3[a-a^{2}+a]^{2}=3[2a-a^{2}]^{2}=3[4a^{2}-4a^{3}+a^{4}]=12a^{2}-12a^{3}+3a^{4}$](/mathtex/e0/e0b3564b8aa6a10d12991fbf3b86ce33.gif)








