Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 03. 2014 09:54
Re: rozvoj funkce
Ahoj.
Bylo by dobré popsat to podrobněji.
Prozatím se zdá být jasné, že pravá strana závisí na  , tudíž
, tudíž  je funkcí proměnné
je funkcí proměnné  . Co jsou
. Co jsou 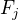 ?
?
Konstanty či nějaké funkce (proměnné  ) ? Pokud by to měly být konstanty (vzhledem k proměnné
) ? Pokud by to měly být konstanty (vzhledem k proměnné  ),
),
pak by šlo o Maclaurinův resp. Taylorův rozvoj funkce  .
.
Offline
#4 09. 05. 2014 10:47
Re: rozvoj funkce
↑ Honza90:
Možná, že jde o nějaký konkretní typ Fourierova rozvoje funkce  , když
, když 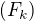 je zvolený (úplný) ortogonální systém.
je zvolený (úplný) ortogonální systém.
Offline
#5 09. 05. 2014 15:48 — Editoval Honza90 (09. 05. 2014 15:49)
Re: rozvoj funkce
↑ Rumburak:
Jedná se o poruchovou řadu(perturbation series)http://en.m.wikipedia.org/wiki/Perturbation_theory
Fn jsou sfericke harmoniky.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline

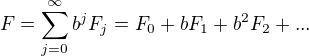
 . b je konstatnta menší než 1, F není funkcí b. Fj mi připadá něco jako eigenfunction..
. b je konstatnta menší než 1, F není funkcí b. Fj mi připadá něco jako eigenfunction..