Matematické Fórum

Wolfram · 27. 07. 2013 15:57

Zdravím, potřebuji poradit s příkladem na kombinatoriku:

Na schůzi má vystoupit pět řečníků A, B, C, D, E. Určete:

A) Kolik je všech možností pro pořadí jejich proslovů
B) Kolik je všech pořadí jejich proslovů takových, že řečník B mluví ihned po A
C) Kolik je všech pořadí jejich proslovů takových, že řečník B mluví po A

vanok · 27. 07. 2013 16:10 — Editoval vanok (27. 07. 2013 17:04)

Ahoj ↑ Wolfram:,
Tu je mi tazko davat rady na najdenie riesenia; tak ti davam strucne riesenie:
A) 5!=120 moznosti
C) Mozne konfiguracie
ABxxx, xABxx, xxABx, xxxAB,
AxBxx, xAxBx, xxAxB,
AxxBx, xAxxB,
AxxxB
Kazda konfiguracia sa vyskitne v 3!=6 pripadoch.
Cize o total mame 10. 3! =60 takych pipadov

B) podobne ako C
uvaz tieto konfiguracie
ABxxx, xABxx, xxABx, xxxAB

JohnPeca18 · 27. 07. 2013 16:42

↑ vanok:
Myslim, ze v B) si pocital v skutocnosti variantu C)
Pretoze zadani B) zni B mluví ihned po A.

↑ Wolfram:
B) Predstavim si, ze recnici B a A jsou jeden recnik a permutuju teda 4 prvky
z toho mam 4!=24 moznosti

marnes · 27. 07. 2013 16:53

↑ Wolfram:
a) už bylo řečeno
b) jestliže má B ihned po a, tak tuto dvojici nahraˇme třeba X. Pak tedy máme X C D E a když vytvoříme jakoukoliv variantu, tak máme při použití X zajištěno, že splníme podmínku

c) uvědomme si, že pro všechny varianty jsou jen dvě možnosti. A to že budˇje AB nebo BA a těch možností musí být stějně. Takže stačí a) dělit dvěma

vanok · 27. 07. 2013 17:02

↑ JohnPeca18:
preklep opraveny

zdenek1 · 27. 07. 2013 20:58

↑ Wolfram:
Ještě k C)
můžeš vypisovat možnosti jako ↑ vanok:, ale také můžeš udělat kombinatorickou úvahu
vybereme pozice pro A a B, tj. z 5 pozic vybereme 2, tj. 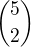${5\choose2}$ možností. Na tyto dvě vybrané pozice můžeme A a B umístit vždy jen jedním způspöbem. Zbylé tři umísťujeme na tři pozice a záleží na pořadí, tj 3! (permutace)
Podle pravidla kombinatorického součinu máš
${5\choose2}\cdot3!$

debi320 · 10. 01. 2014 16:33

Ahoj, úplně si nevím rady s tímto příkladem. Je na kombinatoriku:
"Určete počet všech čtyřciferných přirozených čísel dělitelných čtyřmi, v nichž se vyskytují pouze cifry 1,2,3,4,5."
(Zkoušela jsem to vypočítat, a vyšlo mi 120, ale nevím zda je to celý výsledek, a jestli je to dobře :( ). Předem dík za radu a odpověď :)

gadgetka · 10. 01. 2014 17:03

$5\cdot V^{\prime}(2; 5) = 125$

debi320 · 10. 01. 2014 17:08

↑ gadgetka: : děkuji moc :)

Peterslovak · 10. 01. 2014 17:28

ftp://gw.oacb.cz/PROJEKT/MAT/3_R/Kombin … mutace.pdf

jelena · 09. 05. 2014 09:46

↑ naty085:

Zdravím, jsi na fóru nová - je třeba si založit vlastní téma na každý dotaz (úlohu) a pokusit se podrobněji popsat svůj problém - co jsi zkoušela, jaké máš materiály, napsat i pokus o řešení (může být s chybou, to se prodiskutuje) viz pravidla. Vhodné materiály najdeš v úvodních tématech sekce SŠ, zejména v tématu.

Děkuji.

naty085 · 09. 05. 2014 12:48

↑ jelena:
Dobrý den, ano jsem tady nova tak se omlouvám. Chybu napravim! Děkuji za upozornění.

jelena · 09. 05. 2014 18:13

↑ naty085:

také děkuji, jen jsi měla zakládat "1 téma" = "1 úloha" (ne 4 úlohy do jednoho tématu), sama vidíš, že v tom tématu už se dá obtížně orientovat.

Matematické Fórum

#1 27. 07. 2013 15:57

Kombinatorika

#2 27. 07. 2013 16:10 — Editoval vanok (27. 07. 2013 17:04)

Re: Kombinatorika

#3 27. 07. 2013 16:42

Re: Kombinatorika

#4 27. 07. 2013 16:53

Re: Kombinatorika

#5 27. 07. 2013 17:02

Re: Kombinatorika

#6 27. 07. 2013 20:58

Re: Kombinatorika

#7 10. 01. 2014 16:33

Re: Kombinatorika

#8 10. 01. 2014 17:03

Re: Kombinatorika

#9 10. 01. 2014 17:08

Re: Kombinatorika

#10 10. 01. 2014 17:28

Re: Kombinatorika

#11 09. 05. 2014 09:26 Příspěvek uživatele naty085 byl skryt uživatelem naty085.

#12 09. 05. 2014 09:46

Re: Kombinatorika

#13 09. 05. 2014 12:48

Re: Kombinatorika

#14 09. 05. 2014 18:13

Re: Kombinatorika

Zápatí