Matematické Fórum

těžký, takhle z hlavy · 02. 02. 2009 13:02

Mohl by jste mi někdo poradit jak postupovat v příkladu: Rozložte polynom x^4 - 4x^3 + 11x^2 - 14x + 10 , víme-li, že jedním z kořenů je 1+i

marnes · 02. 02. 2009 13:19

↑ těžký, takhle z hlavy:
Pokud je kořen 1+i, tak je kořenem i komplexně sdružené 1-i, tudíž je polynom dělitelný mnohočlenem
x^2-2x+2 (což je součin (x-(1+i)).(x-(1+i)) ). Po vydělení vyjde x^2-2x+5, což je kvadraticka rovnice řešitelná v C s kořeny opět komplexně sdruženými, které už vypočítáš

těžký, takhle z hlavy · 03. 02. 2009 00:22

↑ marnes:
Takže výsledek je (1+i)(1-i)(1+2i)(1-2i) jestli jsem tam někde neudělal početní chybu.

Martin Korálek · 10. 02. 2009 15:45

↑ marnes:

Mohl bych vědět, proč zrovna (x-(1+i)).(x-(1+i))??

Marian · 10. 02. 2009 15:50

↑ Martin Korálek:
$x^2-2x+2=(x^2-2x+1)+1=(x-1)^2+1=(x-1)^2-\mathrm{i}^2=(x-1-\mathrm{i})\cdot (x-1+\mathrm{i}).$
Je tam chyba ve výpočtu nahoře, takže proto se ptáš zřejmě.

Martin Korálek · 10. 02. 2009 16:16

↑ Marian:

No mě zajímalo, proč odčítam i+1 a i-1 od x? V tomto případě (x-(1+i)).(x-(1+i))

musixx · 10. 02. 2009 16:50

↑ Martin Korálek: Vzdyt uz je to vyse vsechno napsano. Takze jeste jednou: kdyz je korenem nejakeho polynomu s realnymi koeficienty komplexni cislo 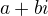$a+bi$ , kde to $b$ neni nula (tedy tam "nejake icko je"), tak z teorie se vi, ze uz musi byt korenem i cislo komplexne sdruzene, tedy $a-bi$ .

Kdyz je korenem polynomu cislo $c$ (at uz je to cislo realne, komplexni nebo buhvijake), tak je poynom delitelny polynomem $x-c$ . Odtud se tedy bere to minus.

Je-li tedy korenem cislo $1+i$ , pak je korenem tez cislo $1-i$ a bavime se po polynomu $(x-(1+i))(x-(1-i))$ .

Martin Korálek · 10. 02. 2009 17:00

↑ musixx:

Jasný, ale když vemu podobný příklad, kde je udávaný kořen taky i+1, tak proč mi dělení vychází se zbytkem?

Zadání je tedy
$x^4+3x^3+3x^2-2$

Daniela_H · 10. 02. 2009 19:57

↑ Martin Korálek:

To by mě také zajímalo. Zkoušela jsem to vydělit a vyjde zbytek 12x-24. Nevíte co s tím? To jsem myslela, že toto umím. Tady člověka dokážete vyvést z omylu :)

Pavel Brožek · 10. 02. 2009 20:03

Pokud jsem dobře počítal, tak i+1 není kořen polynomu $x^4+3x^3+3x^2-2$ .

Daniela_H · 10. 02. 2009 20:06

↑ BrozekP:

A jak jsi na to přišel? Že ti po dělení vyšel zbytek?

Pavel Brožek · 10. 02. 2009 20:09

↑ Daniela_H:

Já jsem to nedělil. Do toho polynomu jsem dosadil i+1 (↑ Martin Korálek: psal, že to je kořen, tak by měla vyjít nula) a vyšlo mi nenulové číslo. Takže je logické, že po vydělení polynomu výrazem (x-(i+1)) zůstane zbytek.

Daniela_H · 10. 02. 2009 20:13

↑ BrozekP:

Aha, takže tam bude asi chybný zadání. Díky za vysvětlení, jsi dobrej ;)

Matematické Fórum

#1 02. 02. 2009 13:02

rozložení polynomu

#2 02. 02. 2009 13:19

Re: rozložení polynomu

#3 03. 02. 2009 00:22

Re: rozložení polynomu

#4 10. 02. 2009 15:45

Re: rozložení polynomu

#5 10. 02. 2009 15:50

Re: rozložení polynomu

#6 10. 02. 2009 16:16

Re: rozložení polynomu

#7 10. 02. 2009 16:50

Re: rozložení polynomu

#8 10. 02. 2009 17:00

Re: rozložení polynomu

#9 10. 02. 2009 19:57

Re: rozložení polynomu

#10 10. 02. 2009 20:03

Re: rozložení polynomu

#11 10. 02. 2009 20:06

Re: rozložení polynomu

#12 10. 02. 2009 20:09

Re: rozložení polynomu

#13 10. 02. 2009 20:13

Re: rozložení polynomu

Zápatí