Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Pravděpodobnost tažení úlohy; úloha však už nemusí v množině být
#1 13. 05. 2014 16:19
Pravděpodobnost tažení úlohy; úloha však už nemusí v množině být
Zdravím, při závěrečných zkouškách tahám 1 úlohu. Typů úloh je šest funguje to tak, že se losuje podle abecedy, s tím že 1. tahá z 20, 2. z 19, 3. z 18 .... poslední ze 2(jedna úloha je navíc).
Zastoupení úloh z oboru A, B jsou po 4 úlohách, z oborů C, D, E, F po 3, tudíž pravděpodobnosti jsou následující:
A - 0,4; B - 0.,4; C - 0,15; D - 0,15; E - 0,15; F - 0,15
Teď už k příkladu. Jde nějak spočítat, jaká je pravděpodobnost že když tahám jako 9. v pořadí , že na mě zbyde třeba ještě úloha z oboru C, přestože nevím, zda už není vytažena?
Předem děkuji.
Offline
#3 13. 05. 2014 18:02 — Editoval Anonymystik (13. 05. 2014 18:04)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Pravděpodobnost tažení úlohy; úloha však už nemusí v množině být
↑ Vašek: Když já nevím, jestli nezaměňuješ 2 různé otázky:
a) jaká je pravděpodobnost, že na mě zbude otázka typu C (tj. že principiálně možné, abych si ji vytáhl)
b) jaká je pravděpodobnost, že si vytáhnu otázku C?
Podle mě jsi odpověděl na otázku b), ale kolega jinsun se ptal spíš na otázku a) (takto jsem tu formulaci pochopil).
--
↑ jinsun:
K mému řešení: představ si, že si ty lidi očísluješ 1, 2, ..., 20 a vybíráš si 3, kterým dáš otázku C. Kolika způsoby to můžeš udělat? Jedná se výběr tří prvků z dvaceti, na pořadí nezáleží (nerozlišuju jednotlivé otázky typu), takže máme kombinace, takže (20 nad 3). A teďka: kolika způsoby můžeš realizovat, otázky typu C dostanou pouze lidé 1, 2, ..., 8 ? No přece (8 nad 3). Čili počet všech možností je (20 nad 3), počet nevyhovujících možností je (8 nad 3), takže pravděpodobnost, že už nic nezbude, je (8 nad 3)/(20 nad 3). Pravděpodobnost, že něco zbude, je doplněk do čísla 1, tedy 1 - (8 nad 3)/(20 nad 3).
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#4 13. 05. 2014 19:15
Re: Pravděpodobnost tažení úlohy; úloha však už nemusí v množině být
↑ Anonymystik:
otázku jsi pochopil dobře :), jinak díky moc. Vyšlo mi, že pravděpodobnost, že na mě zbude typ C je 0,95 není to moc? takhle jsem to počítal: 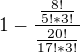
Offline
#5 13. 05. 2014 21:20
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Pravděpodobnost tažení úlohy; úloha však už nemusí v množině být
↑ jinsun: Ano, to vypadá dobře. :-)
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Pravděpodobnost tažení úlohy; úloha však už nemusí v množině být
