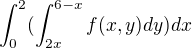Matematické Fórum

hakrt · 15. 05. 2014 15:09

Zdravím,

Dokázal by mi někdo vysvětlit jak se přehazují integrační meze (integrál přes obecnou množinu)

Příklad:

$\int_{0}^{4}(\int_{0}^{y/2}f(x,y)dx)dy+\int_{4}^{6}(\int_{0}^{6-y}f(x,y)dx)dy$

Výsledek:

$\int_{0}^{2}(\int_{{2x}}^{6-x}f(x,y)dy)dx$

Děkuji

vnpg · 15. 05. 2014 17:32 — Editoval vnpg (15. 05. 2014 17:38)

V případě toho prvního integrálu integrujeme přes množinu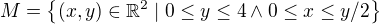

$M = \{ (x,y) \in \mathbb{R}^2 \mid 0 \leq y \leq 4 \land 0 \leq x \leq y/2 \}$ .

Protože protože všechna x a y splňující y <= 4 a x <=y/2 zároveň splňují také x <= 2, můžeme napsat

$M = \{ (x,y) \in \mathbb{R}^2 \mid 0 \leq y \leq 4 \land 0 \leq x \leq 2 \land x \leq y/2 \}$

- tím je definice množiny M nezměněna (jen jsme přidali podmínku, která z těch ostatních plyne automaticky). Dále se všimneme, že podmínku 0 <= y můžeme vypustit, protože plyne automaticky z těch ostatních (konkrétně 0 <= 2x <= y). Tedy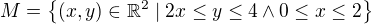

$M = \{ (x,y) \in \mathbb{R}^2 \mid 2x \leq y \leq 4 \land 0 \leq x \leq 2 \}$ .

Tím jsme získali alternativní vyjádření pro množinu M a můžeme napsat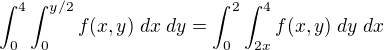

$\int_0^4 \int_0^{y/2} f(x,y) \;dx\; dy = \int_0^2 \int_{2x}^4 f(x,y) \;dy\; dx$ .

(Pro úplnost je třeba zkontrolovat, zda funkce f splňuje požadavky dané Fubiniho větou. To není problém např. v případě, že f je spojitá na M, vzhledem ke kompaktnosti M.)

Nyní zkus upravit stejným způsobem i druhý integrál. Zbytek už je snadný.

Edit: Ještě bych doplnil, že mnohdy je nejjednodušší si nakreslit množinu, přes kterou chceme integrovat, a s pomocí nákresu pak sestavit podmínky.

Matematické Fórum

#1 15. 05. 2014 15:09

Integrační meze

#2 15. 05. 2014 17:32 — Editoval vnpg (15. 05. 2014 17:38)

Re: Integrační meze

Zápatí