Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 05. 2014 10:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: racionální funkce
Zdravím,
jen pro upřesnění: určitě v zadání je "ryze konvexní" (a ne "ryze lomená")? Podle jmenovatele (jeho rozkladu a nulových bodů) se mi nezdá, že bych tu část s konvexnosti našla. Co kolegové? Děkuji.
Offline
#3 16. 05. 2014 11:18
Re: racionální funkce
Zdravím,
také si myslím, že by to mělo být "ryze lomená".
Jinak úloha nemá řešení. Skutečně, buď 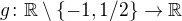 funkce, která je ryze konvexní na každém intervalu, na kterém je definována, a předpokládejme
funkce, která je ryze konvexní na každém intervalu, na kterém je definována, a předpokládejme 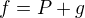 , kde P je polynom. Potom
, kde P je polynom. Potom![kopírovat do textarea $\lim_{x \to -1^+} g(x) = \lim_{x \to -1^+} [f(x) - P(x)] = -\infty$](/mathtex/21/21ee8973962d6d8783fc86cf4cd0aea0.gif)
a podobně 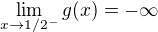 .
.
Z toho plyne, že  není konvexní na intervalu
není konvexní na intervalu 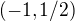 .
.
Offline
