Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Zobecněný Riemannuv Integral - Kritické body (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 05. 2014 12:46
- Evil_Genius

- Zelenáč
- Příspěvky: 9
- Pozice: Student
- Reputace: 0
Zobecněný Riemannuv Integral - Kritické body
Dobrý den, potřeboval bych vysvětlit pojem ''kritické body'' při řešení zobecněných Riemannových integrálů (zkráceně ZRI). Jde o to, že nechápu, proč se některé ZRI rozdělí na 2 integrály pomocí kritického bodu a ani nevím jak se takový kritický bod zjistí. Jak se zjistí ty kritické body (např. v tom prvním příkladě)?
Uvedu 2 příklady:
1.  zde je KRITICKÝM bodem 0, vůbec nevím z čeho se to vyvodilo, že 0 je kritickým bodem
zde je KRITICKÝM bodem 0, vůbec nevím z čeho se to vyvodilo, že 0 je kritickým bodem
2.  zde prý není žádný kritický bod a integrál se řeší normálně - tzn. nemusí se rozdělit na 2 integrály
zde prý není žádný kritický bod a integrál se řeší normálně - tzn. nemusí se rozdělit na 2 integrály
Thanks for your time
Offline
- (téma jako vyřešené označil(a) Evil_Genius)
#2 17. 05. 2014 14:14
Re: Zobecněný Riemannuv Integral - Kritické body
Dobrý den, co jsou to kritické body, je vysvětleno např. zde: http://cs.wikibooks.org/wiki/Integrov%C … egr%C3%A1l
U toho prvního integrálu podle mě 0 není kritický bod - funkce, kterou integrujeme, je v okolí bodu 0 definovaná a navíc i spojitá. Důvodem dělení prvního integrálu pomocí bodu 0 je spíš to, že pak máme možnost použít substituci  . K tomu potřebujeme, aby funkce
. K tomu potřebujeme, aby funkce  byla injektivní na každém z intervalů, přes které integrujeme.
byla injektivní na každém z intervalů, přes které integrujeme.
Je ještě jeden důvod (možná ještě důležitější), proč je někdy třeba rozdělit ZRI od  do
do  . Uvažujme funkci
. Uvažujme funkci  , která je integrovatelná na každém intervalu
, která je integrovatelná na každém intervalu  . Aby byl ZRI
. Aby byl ZRI  dobře definovaný, je třeba, aby existovaly (a byly konečné) ZRI
dobře definovaný, je třeba, aby existovaly (a byly konečné) ZRI 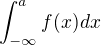 a
a  , kde
, kde 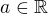 je libovolně zvolené. Pokud
je libovolně zvolené. Pokud  a
a  existují, pak můžeme spočítat
existují, pak můžeme spočítat  jako
jako  (tohle se často uvádí jako definice) nebo jako
(tohle se často uvádí jako definice) nebo jako  , kde
, kde  a
a  jsou libovolné posloupnosti splňující
jsou libovolné posloupnosti splňující  a
a  pro
pro 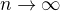 .
.
Je třeba dávat pozor na to, že limita  může existovat a být konečná i přesto, že
může existovat a být konečná i přesto, že  nebo
nebo  neexistuje. V takovém případě ale existence (a v případě existence i hodnota) limity
neexistuje. V takovém případě ale existence (a v případě existence i hodnota) limity  závisí na volbě posloupností
závisí na volbě posloupností  a
a  , takže ZRI
, takže ZRI  není definovaný a je chybou psát
není definovaný a je chybou psát  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Zobecněný Riemannuv Integral - Kritické body (TOTO TÉMA JE VYŘEŠENÉ)