Matematické Fórum

Simon P40 · 23. 05. 2014 22:25

Mám funkci s předpisem:
$\frac{x+3}{9-x^2}$
Definiční obor je $\mathbb{R}-\{\pm 3\}$

Když si ale tu funkci nakreslím, tak vypadá takhle:
//forum.matweb.cz/upload3/img/2014-05/76660_MSP14131eh6187i159755ch00006afcbd6109i0hd7a.gif
Jaktože je v bodě $-3$ definovaná?

JirkaV · 23. 05. 2014 22:30

↑ Simon P40:

Dobrý den,

$9-x^2 = (3-x)(3+x)$

:-) Snad je má rada pochopitelná.

Simon P40 · 23. 05. 2014 22:41

Aha, chápu :)

jelena · 23. 05. 2014 23:58

Zdravím,

podle mne v bodě $x=-3$ definována není, na grafu musí být prázdné kolečko. Souhlasíte? Děkuji.

Simon P40 · 24. 05. 2014 00:00

A nejde o parabolu $\frac{1}{3-x}$ ?

jelena · 24. 05. 2014 00:02

↑ Simon P40:

to je hyperbola, ale úpravu (vykrácení) pro 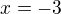$x=-3$ neprovedeš. Pokud jste brali typy nespojitosti, tak bychom takový bod zařadili do odstranitelné nespojitosti.

Simon P40 · 24. 05. 2014 00:47

proč tu úpravu neprovedu? Teď koukám, že i woflram ji provedl a na grafu ten bod má zahrnut. Já nejsem expert matematik, ale když si nevím rady, tak wolframu bezmezně věřím...nechci přijít o iluze :)

JirkaV · 24. 05. 2014 05:52

↑ jelena:

Ano, omlouvám se. Jedná se o bod, který má odstranitelnou spojitost. Musí být zahrnut v D(f).

zdenek1 · 24. 05. 2014 07:12

↑ Simon P40:
Wolframu můžeš věřit, ale musíš mu položit správnou otázku
Odkaz

Na obrázku od Wolframu ta "díra" není vidět, ale def. obor ukazuje, že tam je.

A tu úpravu pro 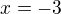$x=-3$ neprovedeš prostě proto, že v tomto bodě původní výraz není definovaný.
A ještě jinak. funkce $f(x)=\frac{x+3}{9-x^2}$ a $g(x)=\frac1{3-x}$ se nerovnají, protože nemají stejný definiční obor. A to je pro rovnost funkcí podmínka nutná.

jelena · 24. 05. 2014 10:24

Simon P40 napsal(a):
tak wolframu bezmezně věřím...nechci přijít o iluze :)

:-) ale pochyboval jsi a vložil sem dotaz. Nakonec se ujasnilo - viz kolegové ↑ JirkaV:, ↑ zdenek1: - děkuji. Jinak z důvodu odlišných definicí "WA nejde věřit" (na příkladech pro SŠ) v otázce liché odmocniny (pokud zápis do WA neupravíš) a v případě funkce arccotg.

JirkaV · 24. 05. 2014 10:40

↑ jelena:

Tak, tak. Wolframu se nemůže na 100% věřit. Důvěřuj, ale prověřuj. :-)

Simon P40 · 24. 05. 2014 11:29

jasný, díky všem!

Matematické Fórum

#1 23. 05. 2014 22:25

Hyperbola a definicni obor

#2 23. 05. 2014 22:30

Re: Hyperbola a definicni obor

#3 23. 05. 2014 22:41

Re: Hyperbola a definicni obor

#4 23. 05. 2014 23:58

Re: Hyperbola a definicni obor

#5 24. 05. 2014 00:00

Re: Hyperbola a definicni obor

#6 24. 05. 2014 00:02

Re: Hyperbola a definicni obor

#7 24. 05. 2014 00:47

Re: Hyperbola a definicni obor

#8 24. 05. 2014 05:52

Re: Hyperbola a definicni obor

#9 24. 05. 2014 07:12

Re: Hyperbola a definicni obor

#10 24. 05. 2014 10:24

Re: Hyperbola a definicni obor

Simon P40 napsal(a):

#11 24. 05. 2014 10:40

Re: Hyperbola a definicni obor

#12 24. 05. 2014 11:29

Re: Hyperbola a definicni obor

Zápatí