Matematické Fórum

nuudle · 20. 05. 2014 19:28

Ahoj,
poradí mi někdo jak vypočítat $\int_{1}^{\infty }\frac{1}{x^{^{2}}-2x+2}$ .

Zasekla jsem se hned na začátku. Rozdělit na parciální zlomky to podle mě nejde a substituce je taky podivná.
Předem díky

misaH · 20. 05. 2014 19:53

↑ nuudle:

Skúsila si MAW?

Oxyd · 20. 05. 2014 19:56

Ten jmenovatel doplň na čtverec, pak lineární substitucí.

Freedy · 20. 05. 2014 20:16

Ahoj,

obecně platí že:
$\int_{}^{}\frac{1}{x^2+a^2}\text{dx}=\frac{1}{a}\text{arctg}(\frac{x}{a})+c$
Když tvůj jmenovatel upravíš na čtverec dostáváš: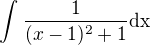
$\int_{}^{}\frac{1}{(x-1)^2+1}\text{dx}$
což se tedy rovná podle výše uvedeného tabulkového integrálu: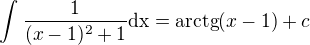
$\int_{}^{}\frac{1}{(x-1)^2+1}\text{dx}=\text{arctg}(x-1)+c$
Tvým úkolem je spočítat určitý integrál s mezemi 1 a nakonečno.
Horní hodnotu odečítáš od dolní tedy musí platit:
$[\text{arctg}(x-1)]^\infty _1 = [\lim_{x\to\infty }\text{arctg}(x-1)] - [\text{arctg(1-1)}]=\frac{\pi }{2}$

Ospli · 20. 05. 2014 20:24

↑ nuudle: Není samotný výraz už parciální zlomek?

jelena · 20. 05. 2014 21:07

↑ Freedy:

Zdravím,

Tobě nefunguje tlačítko Náhled? Potom bys viděl, že zcela dostačující návod k úvodnímu dotazu poskytl kolega v příspěvku nad Tebou.

Freedy napsal(a):
Tvým úkolem je spočítat určitý integrál s mezemi 1 a nakonečno.
Horní hodnotu odečítáš od dolní tedy musí platit:

Toto a následující zápis není korektní - projdeš si to, prosím? Děkuji.

nuudle · 21. 05. 2014 09:14

Ahoj,
díky všem. Hned je to jednoduché.

Btw co se týče toho MAW, tak zkoušela ale hned první krok mi nedával smysl, přeskočila jsem to doplnění na čtverec.

jelena · 21. 05. 2014 09:32

↑ nuudle:

Zdravím a děkuji za zprávu. Pokud je nějaká potíž s MAW, odkaz podpory MAW vede sem do sekce, kde to můžeš prodiskutovat podrobněji. Předpokládám, že Tobě šlo hlavně o počáteční úpravu, bohužel další kroky u ↑ Freedy: nejsou zcela korektní a zatím nemám reakci na ↑ příspěvek 6:.

Freedy · 21. 05. 2014 15:13

Nevím co je nekorektního na počítání integrálu když má jednu z mezí v nekonečnu. Řeší se to pomocí limity nebo ne?

jelena · 21. 05. 2014 22:04

↑ Freedy:

pomocí limity ano, ale porovnej, prosím, Tvůj zápis

$[\text{arctg}(x-1)]^\infty _1 = [\lim_{x\to\infty }\text{arctg}(x-1)] - [\text{arctg(1-1)}]=\frac{\pi }{2}$

s definici nevlastního integrálu (vlivem meze). Našel jsi rozdíl (a odůvodnění, proč je třeba zapisovat jinak)? Děkuji.

Freedy · 25. 05. 2014 06:24

Bohužel ne, jen jsem chtěl zkrátit zápis. Vždyť odečítáme horní meze od dolních. Tak proč né takto?

jelena · 25. 05. 2014 09:59

↑ Freedy:

protože existuje jasně dána definice, která umožní určovat integrál i v případě "nekonečného intervalu". A ta zní - viz 3.1. Ty jsi svým zápisem vynechal podstatu "existuje li vlastní limita $\lim _{u\to b^{-}}\int _{a}^{u}f(x)\, \mathrm{d}x = B$ ... Nekonečno jako mez dosazovat nemůžeš, musí být vysloven (zápisem) předpoklad, že integrál konverguje.

Alespoň tak to vidím. Bylo by dobré, aby si tématu povšiml i někdo z odborných matematiku, pokud bys chtěl diskutovat skutečně na úrovni. Já tu úroveň samozřejmě nemohu poskytnout :-) Kolegům děkuji.

Bati · 25. 05. 2014 10:55

Ahoj,
↑ jelena: má samozřejmě pravdu, $\lim _{u\to b^{-}}\int _{a}^{u}f(x)\, \mathrm{d}x = B$ je standardní způsob definice nevlsatních integrálů.
Tj. v našem případě bychom měli psát
$I=\lim_{M\to\infty}[\text{arctg}\,(x-1)]_1^M=\lim_{M\to\infty}\text{arctg}\,(M-1)-\text{arctg}\, 0$ , což už je to samé, co napsal ↑ Freedy:. Konvergenci tedy apriori řešit nemusíme, ale je vidět i ze zadání.

jelena · 25. 05. 2014 16:00

↑ Bati:

také zdravím a děkuji, kolegovi Freedy s ohledem na jeho seriózní zájem o matematiku, jistě bude vhod diskuse s dalším seriózním zájemcem o matematiku :-)

Matematické Fórum

#1 20. 05. 2014 19:28

Integrál

#2 20. 05. 2014 19:53

Re: Integrál

#3 20. 05. 2014 19:56

Re: Integrál

#4 20. 05. 2014 20:16

Re: Integrál

#5 20. 05. 2014 20:24

Re: Integrál

#6 20. 05. 2014 21:07

Re: Integrál

Freedy napsal(a):

#7 21. 05. 2014 09:14

Re: Integrál

#8 21. 05. 2014 09:32

Re: Integrál

#9 21. 05. 2014 15:13

Re: Integrál

#10 21. 05. 2014 22:04

Re: Integrál

#11 25. 05. 2014 06:24

Re: Integrál

#12 25. 05. 2014 09:59

Re: Integrál

#13 25. 05. 2014 10:55

Re: Integrál

#14 25. 05. 2014 16:00

Re: Integrál

Zápatí