Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2014 12:06
Pravděpodobnost
Ahoj, neví někdo, jak na tento příklad?
Nezkušený otec rozdal čtyřem dětem jejich zubní kartáčky náhodně, protože nevěděl, který komu patří. Určete pravděpodobnost, že alespoň jedno dítě dostalo vlastní kartáček.
Offline
#2 25. 05. 2014 12:31
Re: Pravděpodobnost
↑ barca.fl:
Dobrý den. Řekl bych, že přes doplňkovou pravděpodobnost:
P(aspoň jedno dítě dostane svůj kartáček) = 1 - P(žádné dítě nedostane svůj kartáček).
Pokud se tedy nemýlím.
Offline
#4 25. 05. 2014 18:39
Re: Pravděpodobnost
↑ barca.fl:
Šel bych na to zřejmě přes výpis možností, kdy neplatí žádné správné přiřazení kartáček <--> děcko.
Děcka: A,B,C,D; kartáčky a,b,c,d:
Děcku A přiřadíme např. karáček D a podíváme se na další možnosti:
A B C D
d a b c
a c b
b a c
b c a
c a b
c b a
Je zřejmé, že bez žádného správného přiřazení jsou jen tři (bílé) řádky, to zn. tři možnosti.
Děcku A můžeme ještě přiřadit písmena b, c, v obou případech zase tři možnosti.
Takže je 9 způsobů rozdělení karáčků, kdy není žádné správné přiřazení. Celkový počet
možností rozdělení je 4! = 24.
Takže bych řekl: Pravděpodobnost, že alespoň jedno dítě dostane vlastní kartáček =
Pokud se tedy nemýlím.
Offline


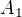 ,
, 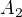 ,
, 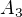 a
a 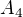 v libovolném pravděpodobnostním prostoru platí
v libovolném pravděpodobnostním prostoru platí .
.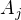 jev, kdy dítě
jev, kdy dítě 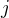 dostane svůj kartáček.
dostane svůj kartáček.