Matematické Fórum

pietro · 23. 05. 2014 10:13

Zdravím :-) , keby sa Vám chcelo....podumať ♜.

Dva mráčiky najrozšírenejšieho prvku vo vesmíre, atomárneho vodíka (nech sú ako ideál. plyn), každý o hmotnosti m, majú počiatočné: vzdialenosť r(0)=R a rýchlosť v(0)=0. Vypočítajte o koľko Kelvinov sa ohrejú pri dokonale nepružnej zrážke. (uvažujme, že sú to kompaktné telesá po celý čas ich gravitačného pôsobenia)
ΔT=f(m,R)=?

niečo na spôsob príkladu napr.
http://forum.matweb.cz/viewtopic.php?id=74565

nemám riešenie, len gravitačnú konštantu a teplotu som vedĺa seba ešte nevidel.

ďakujem.

Brzls · 25. 05. 2014 10:37

Zdravím

Uloha mi přijde pěkná. Nejspíš nebude mít nějaké jednoznačné řešení, bude záležet jaké si kdo zvolí zjednodušující předpoklady a vůbec jak se rozhodne celou situaci modelovat, no a samozřejmě čím reálnější model, tím bude řešení komplikovanější (proto jsem přesunul do Zajímavých).

Já si tedy představuji dvě mračna, s hmotností m, které mají v důsledku vlastní gravitační síly tvar koule.

Vlivem gravitace druhého mračna, se začnou přitahovat, spojí se a utvoří nové mračno, které také bude mít tvar koule.

Později sem přidám svoje řešení, rád bych se koukl jak by to řešili ostatní.

MirekH · 26. 05. 2014 15:04 — Editoval MirekH (28. 05. 2014 08:59)

Zdravím,

asi bych taky uvažoval dvě kulová mračna, která se spojí v jednu větší kouli. Přitom předpokládáme, že počáteční vzdálenost je mnohem větší než rozměr mračen (ideálně nekonečná).

Při řešení bych vycházel z předpokladu, že jednotlivá mračna jsou na začátku i po fúzi v tepelné rovnováze a [s]teplotní[\s] rychlostní rozdělení je maxwellovské. Z kruhové rychlosti bych spočítal hustotní rozložení a z Gausse gravitační potenciální energii. Pokud se po srážce počet částic zachová (žádné neodletí), můžu využít zákona zachování energie a dopočíst střední hodnotu kinetické energie, která přes ekvipartiční teorém odpovídá teplotě.
S újmou na obecnosti zanedbáváme ionizaci.

Skutečně to počítat jsem nezkoušel, ale určitě existuje nějaký jednodušší rozumný model.

Brzls · 27. 05. 2014 14:32 — Editoval Brzls (28. 05. 2014 20:41)

Ahoj

Já osobně jsem uvažoval, že je plynová koule v takovém stavu, že hydrostatický tlak je v rovnosti s tlakem plynu.
V takové situaci je ale ještě nutno dodat nějakou další počáteční podmínku, jako například závislost hustoty na vzdálenosti od středu. (já třeba zkoušel počítat při konstantní hustotě)

Autor skryl část textu. Zobrazit/skrýt!

Je jasné, že vzhledem k dosti zjednodušeným podmínkám jde pouze o jakýsi řádový odhad.

↑ MirekH:

Mohl by si to nějak rozepsat? Například co přesně znamená, že teplotní rozdělení je maxwellovské a co přesně se myslí kruhovou rychlostí? Nevím jestli tomu úplně rozumím

pietro · 27. 05. 2014 20:03

Ahoj,

Ďakujem Vám za podnetné námety !

Mám takú idealizovanú predstavu, že pre tie hmotnosti ( m + m ) by som mal najprv vyrátať rýchlosť ich vzájomnej zrážky.

Jedno m ukotvím pevne do bodu x=0, druhé do x(0)=R, a to druhé uvoľním.
Malo by sa to správať podľa difer. rovnice

http://www.wolframalpha.com/input/?i=x% … 280%29%3D0

Nech sa zrazia rýchlosťou vx < c, ( to docielime vhodnou voľbou x(0))

( plus zanedbať v prvom priblížení ešte relativistický vzťah pre hmotnosť )
=====================================================

Rovničku diferenciálnu , nakopnite ma prosím na jej riešenie ..... nech máme aspoň jednu rýchlosť vx.

Ďakujem pekne :-)

Brzls · 27. 05. 2014 21:04 — Editoval Brzls (27. 05. 2014 21:05)

↑ pietro:

Ahoj

Jenže jak bude potom vypadat další řešení? Tam to komplikuje ten fakt, že se ty mraky spojí do jednoho.
Kdybychom uvažovali, že se nejedná o plynová mračna, ale o dvě pevné tělesa, tak bych tomu rozuměl - prostě spočítám jakou rychlostí do sebe narazí, přírustek energie je roven kinetické energii před sážkou a je to.
Ale pokud jsou to plynová mračna tak nevím jak by to pokračovalo...

Jinak u podobných rovnic se dá snížit řád, když si uvědomíš, že

$\frac{dv}{dt}=\frac{dv}{dx}\frac{dx}{dt}=\frac{dv}{dx}v$

to když tam dosadíš, separuješ proměnné, tak ale stejně nedostaneš nic jiného než zákon zachování mechanické energie.

Takže pokud bys chtěl přesný průběh rychlosti, tak rovnou řešíš diferenciální rovnici ve tvaru zachování energie (tam se také dají separovat proměnné).

Pokud tě zajímá rychlost těles před srážkou, tak ani nemusíš řešit dif. rovnici ale opravdu jen vyjít ze zachování mechanické energie.

MirekH · 28. 05. 2014 09:04

↑ Brzls:
S tou kruhovou rychlostí jsem to myslel tak, že pokud budou částice v plynu splňovat Maxwellovo rychlostní rozdělení (napsal jsem předtím teplotní, opraveno) a pokud budu předpokládat, že se částice pohybují po kružnicích kolem středu mraku jako planety, tak jsem schopen spočítat i rozložení hustoty (aspoň doufám). Jenom nevím, nakolik je ten předpoklad s částicemi pohybujícími se kruhovou rychlostí dobrý – určitě nemohou překonat únikovou rychlost, ale nejsem si zcela jistý, jestli mohu jen tak snadno odvrhnout eliptické dráhy. Asi to není moc dobrý model, byl to jen takový nástřel. Ještě se nad tím zamyslím.

pietro · 28. 05. 2014 12:17

↑ MirekH: vďaka za posun :-)

$\int_{0}^{v_x}vdv=\int_{R}^{R_x}-G.\frac{m}{x^{2}}dx$

$v_x=\sqrt{2.G.m.(\frac{1}{R_x}-\frac{1}{R}})$

Brzls · 28. 05. 2014 15:13

↑ pietro:

Jo a ještě poznámka, nevím jestli jsem to pochopil, ale pokud máš počátek soustavy pevně spojen s jedním tělesem (tedy střed jedné koule je celou dobu v bodě x=0), tak je třeba myslet, že tato soustava je neinerciální. Tedy bylo by uvažovat sílu působící na tu druhou kouli jako dvakrát větší!

darkorbit · 28. 05. 2014 15:58

Ahoj

Práve podobný problém som prednedávnom riešil (neúspešne). Chcel som určiť rozloženie hmotnosti v takomto mraku. Šiel som na to takto. Už sa v diskusii objavilo, že tlak sa správa takto: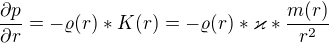
$\frac{\partial p}{\partial r}=-\varrho (r)*K(r)=-\varrho (r)*\varkappa *\frac{m(r)}{r^2}$
Zo stavovej rovnice mám pre hustotu:
$\varrho (r)=\frac{M}{RT}p(r)$
Kde "M" je molová hmotnosť a "R" je plynová konštanta.
Pričom predpokladám, že teplota vrámci mraku je konštantná (postupom času by k tomu malo dôjsť). Po dosadení a úprave rovnice hore mám:
$\frac{dp}{p}=-\frac{\varkappa M}{RT}$
Riešením (integráciou) mám:
$p(r)=Ae^{-\frac{\varkappa M}{RT}\int_{0}^{r}\frac{m(r)}{r^2}dr}$
"A" je nejaká int, konštanta. Teraz si vezmem šupku vo vzdialenosti "r" od stredu. Platí stavová rovnica v tvare:
$p(r)dV=\frac{dm}{M}RT$
Diferenciál objemu viem nahradiť a výsl. rovnica je:
$A4\pi r^2e^{-\frac{\varkappa M}{RT}\int_{0}^{r}\frac{m(r)}{r^2}dr}=\frac{RT}{M}\frac{d}{dr}m(r)$

Tu som skončil pri riešení úlohy. Dúfam, že to niekomu pomôže a zdarne ukončí úlohu. Okrajové podmienky sú už triviálne.

Brzls · 28. 05. 2014 21:07

↑ darkorbit:

Ahoj
Děkuji za další reakci
V tom třetím řádku ti tam jenom nedopatřením vypadlo m(r)/(r^2), pak již s tebou souhlasím (osobně bych řešil jinak resp. dopracoval se k jiné rovnici, ale mělo by to vést na stejný průběh veličin)

Jinak pokud tě nenapadá, jak nějakým rozumným způsobem tu tvojí rovnici vyřešit (mě určitě ne) tak stejně bude potřeba si pomoc nějakým softwarem.

Počáteční podmínky jsou jasné no a další řešení by podle mě postupovalo jak jsem již psal nahoře. Tam jsem psal jen stěžejní rovnice při řešení právě kvůli tomu, že záleží jaké si kdo zvolí podmínky (ty jsi například zvolil konstantní teplotu)

Xellos · 28. 05. 2014 21:21 — Editoval Xellos (29. 05. 2014 15:01)

↑ darkorbit:

Ak by sa polomer neobjavoval nikde v citateli resp. by sme uvazovali len 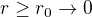$r \ge r_0 \rightarrow 0$ (netuzim po deleni nulou), tak to je lepsie prepisat na difku: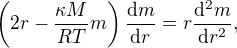

$\left(2r-\frac{\kappa M}{RT}m\right)\frac{\mathrm{d}m}{\mathrm{d}r}=r\frac{\mathrm{d}^2m}{\mathrm{d}r^2},$

ktora ma aspon jedno zmysluplne riesenie: $m=\frac{2RT}{\kappa M}r$ .

↑ Brzls:

Take veci ako konstantna teplota sa daju dobre odovodnit - vseobecne chceme rovnovazny stav v povodnych mrakoch, uz len aby platila stavova rovnica. Nevolime si to ako chceme, ale tak aby v tom bol fyzikalny zmysel.

$\hline$

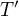Co tak zratat energiu mraku s hmotnostou $m$ a teplotou $T$ voci nulovej hladine "vsetok plyn vo vzdialenosti $r \rightarrow \infty$ a na teplote $T \rightarrow 0$ "? Potom staci uz len trapne $2E(m,T)+E_g=E(2m,T')$ kde $T'$ je hladana teplota a $E_g=-\frac{\kappa m^2}{R}$ (edit: 1/R nie 1/R^2) pot. energia mrakov (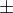 $\pm$ znamienka).

Brzls · 28. 05. 2014 22:11 — Editoval Brzls (29. 05. 2014 16:10)

↑ Xellos:
Zdravím

Jasně že je to dobře odůvodněné, jenže existují i jiné stavy, které vyhovují fyzikálním zákonům a zároveň řešení jsou pro ně mnohem jednodušší. Sice nejsou přesné a ani stabilní, ale kdybychom chtěli řádový odhad a koule by byla dostatečně veliká, tak bych osobně volil předpoklad konstantní hustoty - není to zdaleka tak přesné, ale jen abych měl představu v jakých číslech se to pohybuje tak by mi to stačilo.
A vůbec, myslím že existují i jiné stabilní stavy, kde teplota není konstantní...

Pokud chápu co navrhuješ, tak je to téměř stejné jako to co jsem navrhoval já
1. Určit vnitřní energii (což je při konstantní teplotě triviální)
2. Určit potenciální energii

Nesmíš ale zapomínat, že Eg není jenom
$E_g=-\frac{\kappa m^2}{R}$

ale je třeba uvážit i vlastní potenciální energie obou těch dvou mračen (práce potřebná na utvoření jedné té koule) tedy:
1. Určit průběh hustoty
2. Určit průběh intenzity jak vně koule (triviální) tak uvnitř koule (proto ten průběh hustoty)
3. Určit průběh potenciálu vevnitř koule
4. Určit vlastní energii koule jako
$\frac{1}{2}\int_{M}^{}\varphi dm$

(prostě potenciální energie je energie potřebná na přemístění hmoty z nekonečna do dané polohy - potřebuji energii i na to, abych utvořil tu kouli)

kde fí jsem označil potenciál.
No a tím se nám to samozřejmě komplikuje, takže už to nebude tak trapný :)

Měli jsme na mysli to samé?

Mohu se ještě zeptat jak se dospělo k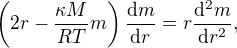
$\left(2r-\frac{\kappa M}{RT}m\right)\frac{\mathrm{d}m}{\mathrm{d}r}=r\frac{\mathrm{d}^2m}{\mathrm{d}r^2},$
?? Není mi to jasné

Děkuji

darkorbit · 28. 05. 2014 22:29

Ďakujem za vyriešenie onej rovnice (Xellosovi), odtiaľto už je to pomerne triviálne. Nedalo by sa ale ešte popísať, akým spôsobom sa k riešeniu dospelo (ak wolframizáciou, tak to netreba písať)?

darkorbit · 29. 05. 2014 09:56

Ahoj,

ten vzťah pre potenciálnu energiu sa mi moc nezdá, ono to má rozmer sily, skôr si myslím, že to je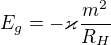
$E_{g}=-\varkappa \frac{m^2}{R_{H}}$
ale to je detail.
Moja otázka je však na BRZLS. Nerozumiem, prečo sa vo výpočte vlastnej potenciálnej energie mraku objavuje tá 1/2 . Ak si to hodím do výpočtov, napočudovanie mi sedia (bez toho nesedia) - prosil by som objasniť.

Ďakujem

pietro · 29. 05. 2014 10:02

↑ Brzls: ďakujem za nasmerovanie , tak to teda upravím

$v_x=\sqrt{4.G.m.(\frac{1}{R_x}-\frac{1}{R}})$

$2E_k=2Q$

nech c=merná tepelná kapacita v J/(kg.K)

$2.\frac{1}{2}mv^{2}_x=2.mc\Delta T$

potom

$\Delta T=2.\frac{Gm}{c}.(\frac{1}{R_x}-\frac{1}{R})$

pietro · 29. 05. 2014 11:54 — Editoval pietro (31. 05. 2014 10:16)

Ešte po doplnení mernej tepelnej kapacity
1 častica atomárneho vodíka

(k= Boltzmann konšt.)

cv=(3/2)*k (J/K)
cp=(5/2)*k (J/K)

nech hmotnosť 1 atomu je mH v kg
potom kapacita na kilogram

V=konšt.... c1= (3/2)*(k/mH) (J/kgK)
p=konšt.... c2= (5/2)*(k/mH) (J/kgK)

a nech R--> inf.

$\Delta T=\alpha .\frac{G.m.m_H}{k.R_x}$ kde $\alpha =(4/3 resp. 4/5)$ (izochor resp. izobar)

(teplý gravitačný dotyk :-)

Xellos · 29. 05. 2014 15:21 — Editoval Xellos (29. 05. 2014 15:22)

↑ Brzls:

No ked chceme radovy odhad tak sa uloha dost zjednodusi. Az exaktne riesenie je challenge :D

Co si predstavujes ako stabilny stav kde teplota nie je konstantna? Ja si ziadny neviem predstavit, po nekonecnom case by sme (za predpokladu ze vodik je inertny) furt mali dostat len izotermicky idealny plyn...

Vlastna pot. energia je zahrnuta v slovach

Xellos napsal(a):
vsetok plyn vo vzdialenosti $r \rightarrow \infty$

(a hej, ma tam byt 1/R a nie 1/R^2); ak pozname rozlozenie hmoty (to linearne vyzera fyzikalne ok) tak je zvysok len par trapnych integralov ako pises. Ale nevidim preco 2-ka v energii.

Ako som dospel k difke? Zlogaritmuj a zderivuj obe strany, je to dost lahke ked pouzijes $\log{xy}=\log{x}+\log{y}$ .

↑ pietro:

Naopak, $c_p=R+c_V$

Brzls · 29. 05. 2014 16:44 — Editoval Brzls (29. 05. 2014 16:52)

↑ darkorbit:

K té energii:
Když uvážíš například dva hmotné body hmotnosti m1 a m2, tak každý kolem sebe bude vytvářet pole s potenciálem fí1 a fí2.
Energie této soustavy je pak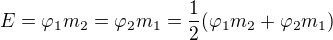
$E=\varphi _{1}m_{2}=\varphi _{2}m_{1}=\frac{1}{2}(\varphi _{1}m_{2}+\varphi _{2}m_{1})$
To se dá zobecnit s ohledem na libovolný počet hmotných bodů
$E=\frac{1}{2}\sum_{i,j}^{}\varphi _{i}m_{j}$ (i se nerovné j a oba indexi probíhají od nuly do n)
a to přímočaře zobecnit na
$E=\frac{1}{2}\int_{M}^{}\varphi dm$
To je energie jednoho tělesa s hmotností m.

↑ Xellos:
No mě je v tom stejně o něco víc než pár trapných integrálů:
Předpokládám, že počáteční rozměry a počáteční teplota koulí jsou zadané.
Pak celková energie Ec (gravitační i vnitřní) těchto koulí záleží jak na poloměru té koule a teplotě.
Pakliže jsou zadané, jsem schopen výše popsaným postupem tuto energii stanovit.
Ale...

Potom, co do sebe koule narazí, tak neznám ani nový rozměr nové koule, ani novou teplotu této koule.
Energie této koule závisí pouze na této nové teplotě a novém poloměru.

To znamená, že ze zachování energie mám pouze jednu rovnici pro dvě neznámé... Nebo se pletu?

Teda teď koukám na předchozí příspěvky a vidím, že tu rovnici řeší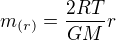
$m_{(r)}=\frac{2RT}{GM}r$

Tím bych měl i tu druhou rovnici a je pravda že pak by to bylo jen pár integrálů navíc.
Ale jak dokázat, že rovnici neřeší žádná jiná další funkce, nebo alespoň žádné jiné řešení nemá fyzikální smysl. Mě to totiž moc jasné nepřijde. Pokud by se to dalo dokázat, tak bych již úlohu považoval za vyřešenou.

Co se týče té nekonstantní teploty tak se nechci pouštět do diskuze, neboť si sám nejsem jistý jestli mám pravdu, musím si to promyslet. Tak či tak konstantní teplota je nejlepší předpoklad :)

Brzls · 29. 05. 2014 17:07 — Editoval Brzls (29. 05. 2014 17:11)

↑ Xellos:

Teď vidím že to řešení je značně "podezřelé"

Ty úpravy které použiješ při té úpravě mají smysl pouze tehdy, když existuje limita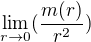
$\lim_{r\to0}(\frac{m(r)}{r^{2}})$
Právě kvůli problému s dělením nulou. Tomu ale to lineární řešení rozhodně nevyhovuje.
To si navíc můžeme ověřit tím, že uděláme zkoušku a zkusíme dosadit do původní rovnice.
(když přehlédneme, že dam dostaneme neexistující nevlastní integrál a položíme ho nekonečnu, tak to stejně nebude sedět)

Takže je podle mě potřeba hledat jiný průběh funkce m(r), neboť to lineární nevyhovuje zkoušce a ten postup jak se k němu dospělo (právě to dělení nulou) je krajně pochybný...

darkorbit · 29. 05. 2014 17:09

Trochu som pracoval s riešením od Xellosa a príde mi pochybné, že pri zvýšení teploty mraku predpovedá pri zachovaní hmotnosti zmenšenie polomeru mraku, pretože platí pre úhrnnú hmotnosť a celkový polomer:
$R_{H}=\frac{\varkappa M_{m}M}{2R_{m}}\frac{1}{T}$
Kde "M" je úhrnná hmotnosť. Deriváciou plynie, že pri zvýšení teploty klesne polomer. Nedokážem k tomu vymyslieť fyziku izodejov, t.j. nejak mi to nesedí k rovnici
$\delta Q=dW+dU$
Pretože zahrievanie si predstavujem ako dodanie tepla - to je aj zrážka tých mrakov, pričom vykonaná práca plynu je vlastne zmena pot. energie, tá však pri zmenšení polomeru klesá, teda plyn vykoná zápornú prácu???

Ak je chyba v mojich úvahách, tak ma prosím opravte.

pietro · 29. 05. 2014 17:41

↑ Xellos: vďaka za opravu....:-)

darkorbit · 29. 05. 2014 18:58

↑ Brzls:

Skúšal som riešiť tú pôvodnú rovnicu jej priamočiarou deriváciou a spätným dosadením vyjadrenia tej nechutnej exponenciály pomocou derivácie hmotnosti a dostal som rovnicu podobnú, ako Xellos, ale predsa rozdielnu:
$(2r-\frac{\varkappa M}{RT}m(r))\frac{dm(r)}{dr}=r^{2}\frac{d^2m(r)}{dr^2}$
Táto mi príde správnejšia, pretože (aspoň zdanlivo) majú obe strany rovnaký rozmer (kg), čo Xellosova difka nespĺňa. Problém teraz je, že žiaden software mi to ešte nezriešil.
Nemáte niekto nejaký nápad??

Xellos · 29. 05. 2014 19:16

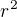Tak $r^2$ , whatever.

Predtym ako sa snazite vyvratit tvrdenie, skontrolujte si ci ste si ho neupravili :D Netvrdim ze existuje linearne riesenie povodneho problemu, ale difky ktoru som tam napisal (a tiez som spomenul ze plati len ak sa obmedzime na $r \ge r_0$ ). Mne sa zda dost pofiderne, ze by hnusna difka mala jednoduche riesenie... uz len intuicie riesitela... ale stale to nie je dovod toto riesenie nespomenut.

Mozno by bolo rozumnejsie to rovno nakodit.

Xellos · 29. 05. 2014 19:22

↑ Brzls:

To mas zle, potrebujeme aby existovala (konecna, pravostranna) limita v nule od primitivnej funkcie z integralu v exponente, teda od $\log{r}$ . Protipriklad: $m(r)=r^{\frac{3}{2}}$ , limita $r^{-\frac{1}{2}}$ v nule konecna urcite nebude, ale $\int_{0}^r{\frac{m(r)}{r^2}}=\left.2\sqrt{r}\right|_0^r$ existuje.

Neskusaj ma tromfnut v analyze :D

Matematické Fórum

#1 23. 05. 2014 10:13

dva mraky

#2 25. 05. 2014 10:37

Re: dva mraky

#3 26. 05. 2014 15:04 — Editoval MirekH (28. 05. 2014 08:59)

Re: dva mraky

#4 27. 05. 2014 14:32 — Editoval Brzls (28. 05. 2014 20:41)

Re: dva mraky

#5 27. 05. 2014 20:03

Re: dva mraky

#6 27. 05. 2014 21:04 — Editoval Brzls (27. 05. 2014 21:05)

Re: dva mraky

#7 28. 05. 2014 09:04

Re: dva mraky

#8 28. 05. 2014 12:17

Re: dva mraky

#9 28. 05. 2014 15:13

Re: dva mraky

#10 28. 05. 2014 15:58

Re: dva mraky

#11 28. 05. 2014 21:07

Re: dva mraky

#12 28. 05. 2014 21:21 — Editoval Xellos (29. 05. 2014 15:01)

Re: dva mraky

#13 28. 05. 2014 22:11 — Editoval Brzls (29. 05. 2014 16:10)

Re: dva mraky

#14 28. 05. 2014 22:29

Re: dva mraky

#15 29. 05. 2014 09:56

Re: dva mraky

#16 29. 05. 2014 10:02

Re: dva mraky

#17 29. 05. 2014 11:54 — Editoval pietro (31. 05. 2014 10:16)

Re: dva mraky

#18 29. 05. 2014 15:21 — Editoval Xellos (29. 05. 2014 15:22)

Re: dva mraky

Xellos napsal(a):

#19 29. 05. 2014 16:44 — Editoval Brzls (29. 05. 2014 16:52)

Re: dva mraky

#20 29. 05. 2014 17:07 — Editoval Brzls (29. 05. 2014 17:11)

Re: dva mraky

#21 29. 05. 2014 17:09

Re: dva mraky

#22 29. 05. 2014 17:41

Re: dva mraky

#23 29. 05. 2014 18:58

Re: dva mraky

#24 29. 05. 2014 19:16

Re: dva mraky

#25 29. 05. 2014 19:22

Re: dva mraky

Zápatí