Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2014 18:57
nerovnice s absolutní hodnotou
Ahoj, zrovna si opakuji kapitolu nerovnice s absolutní hodnotou. Tuto kapitolu mám již dávno za sebou. Všiml jsem si před nedávnem, že po každé, když rozděluji absolutní hodnotu na dva případy, tak v druhém případě již nepoužívám zobáček i s rovnítkem. Ten vídávám všude možně na netu. Tedy v tomto př. používám pouze  místo
místo  . Nepamatuji si, že by mi někdo toto vytkl. Nevzpomínám si ,že bych měl obtíže s abs. hodnatami To v zásadě nemá nikdy vliv na konečný výsledek ne?. Je to OK ?:)
. Nepamatuji si, že by mi někdo toto vytkl. Nevzpomínám si ,že bych měl obtíže s abs. hodnatami To v zásadě nemá nikdy vliv na konečný výsledek ne?. Je to OK ?:)
1)



2)




Offline
- (téma jako vyřešené označil(a) bonifax)
#4 29. 05. 2014 19:09 — Editoval gadgetka (29. 05. 2014 19:12)
Re: nerovnice s absolutní hodnotou
Ahoj, nás kdysi profesor matematiky učil, že v intervalu, pro který řešíš dílčí nerovnice, má být neostrá nerovnost, čili  nebo
nebo  , protože by se mohlo stát, že by utekl nějaký kořen nerovnice. Je to hlavně v takových dílčích řešeních, která na sebe navazují a jsou např.
, protože by se mohlo stát, že by utekl nějaký kořen nerovnice. Je to hlavně v takových dílčích řešeních, která na sebe navazují a jsou např.  a
a  a
a  . Když se interval bere jen v kulatých závorkách, krajní body řešení by utekly a místo
. Když se interval bere jen v kulatých závorkách, krajní body řešení by utekly a místo 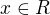 bys pak měl řešení
bys pak měl řešení  .
.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#5 29. 05. 2014 19:11
Re: nerovnice s absolutní hodnotou
↑ bonifax:
Ahoj.
Ak je číslo v absolútnej hodnote rovné nule, tak je nula aj absolútna hodnota.
Oplatí sa využiť, že napríklad ak  , tak
, tak  .
.
Potom aj pre  platí
platí  .
.
Po pripočítaní čísla 6 k obom stranám nerovníc dostaneme hneď  , odtiaľ
, odtiaľ 
Offline
#6 29. 05. 2014 19:23
Re: nerovnice s absolutní hodnotou
↑ bonifax:
Tvůj postup v příspěvku #1 je naprosto v pořádku a je to přímo učebnicový postup i s tím kde používáš  ,
,  .
.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 29. 05. 2014 19:25 Příspěvek uživatele bonifax byl skryt uživatelem bonifax. Důvod: ?X
#8 29. 05. 2014 19:32
Re: nerovnice s absolutní hodnotou
↑ zdenek1:
takže i v libovolném příkladě nerovnice s Ab. hodnotou, použiji-li 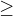 poté , je to OK?:)
poté , je to OK?:)
Offline
#9 29. 05. 2014 19:40
Re: nerovnice s absolutní hodnotou
↑ bonifax:
To se takto obecně nedá říct, zejména pokud je těch absolutních hodnot více. Důležité je aby každá hranice v nějakém intervalu byla.
To co ukazuje ↑ gadgetka: v #4 je bezpečné.
Na druhou stranu, když použiješ ,
,  ,
, 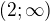 ,
,
tak to určitě není špatně a je to klasické dělení intervalů podle definice.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#10 29. 05. 2014 19:58
Re: nerovnice s absolutní hodnotou
↑ zdenek1:
dobře tedy, tedy suma sumarum, používat zobáček pro druhej příklad je tedy bezpečnější. Já si nechám postup ten, který jsem dělal doposud a jen si dát pozor na ty hranice ok :)
Děkuji všem za reakce a mějte se pěkně!
Offline

