Matematické Fórum

Není to korektní, vy chcete odadnout dva parametry z jednoho pozorování. Rozumnější bude požádat dodavatele o cen. nabídku i pro tento případ.

Na základě informací, které máme k dispozici, můžeme pouze odvodit, že cena za konfiguraci 8(x1) + 8(x2) splňuje nerovnosti (za předpokladu linearity, tj. např. že nejsou žádné slevy za nákup většího množství, a za předpokladu, že všechny ceny jsou kladné). Přitom hodnota je blízko 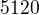v případě, že cena za (x2) je mnohem nižší než cena za (x1), a naopak je blízko 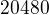, pokud cena za (x2) je mnohem vyšší než cena za (x1).

Abychom mohli učinit přesnější závěry, potřebovali bychom znát např. nějaký vztah mezi cenami (x1) a (x2). Kdybychom např. znali cenu za konfiguraci a(x1) + b(x2), kde vektor (a,b) není skalárním násobkem vektoru (8,2), pak bychom mohli za předpokladu linearity spočítat přesnou cenu .

Mám bláznivú teóriu, ale ktorá +/- autobus sedí.

Mám sústavu rovníc (staršia cenová ponuka z iného zdroja)
0,5(x1) + 0,5(x2)=1 230
0,5(x1) + 1(x2)=1 490
0,5(x1) + 2(x2)=1 740
0,5(x1) + 3(x2)=2 040
1(x1) + 1(x2)=2 150
1(x1) + 2(x2)=2 460
1(x1) + 4(x2)=2 980
1(x1) + 6(x2)=3 480

Teraz z každej rovnice vyjadrím (x1) a (x2) takto napr. z prvej rovnice
x(1) 1 230/0,5 = 2460 a x(2) 1230/0,5 = 2460

dostanem novú sústavu

0,5*2 460     + 0,5*2 460 = 4920
0,5*2 980    + 1*1 490 = 4 470
0,5*3 480    + 2*870 = 4 350
0,5*4 080    + 3*680 = 4760
1,0*2 150    + 1*2 150 = 4 300
1,0*2 460    + 2*1 230 = 3 690
1,0*2 980    + 4*745 = 3 720
1,0*3 480    + 6*580 = 4 060

Je vidno, že výsledok každej rovnice je dvojnásobný. Takže podelím číslom 2 (x1), (x2) a výsledok a dostanem

0,5*1 230     + 0,5*1 230 = 1 230
0,5*1 490    + 1*745 = 1 490
0,5*1 740    + 2*435 = 1 740
0,5*2 040    + 3*340 = 2 040
1,0*1 075    + 1*1 075 = 2 150
1,0*1 230    + 2*615 = 2 460
1,0*1 490    + 4*372,5 = 2 980
1,0*1 740    + 6*290 = 3 480

Podľa MNŠ v Mathcade vyšlo (x1) = 1 976 a (x2) = 273.
Podľa MNŠ v Exceli (plus zvyšok) (x1) = 1 397, (x2) = 273 a zvyšok 482.
Podľa mojej "teórie" spriemerujem hodnoty kde (x1) = 1 504 a (x2) = 637.

Dosadím pre hodnotu 1*(x1) + 1*(x2):
1, 1* 1 976 + 1* 273 = 2 249
2, 1*1 397 + 1*273 + 482 = 2 152
3, 1*1 504 + 1*637 = 2 141

Takže +/- autobus to sedí.

Aplikujem rovnaký spôsob na moju pôvodnú rovnicu (žiaľ je len jedna):

(x1)=5 120/8 = 640

(x2) = 5120/2 = 2 560

Dosadím do základnej rovnice :

8*640 + 2*2 560 = 5 120 + 5 120 = 10 240

Vyšlo mi to presne dvojnásobok základnej rovnice. Takže (x1), (x2) a y podelím dvomi

8*320 + 2*1 280 = 2 560 +2560 = 5 120

z toho vyplýva (x1) = 320 a (x2) = 1 280.

A teraz podstatná vec. Ja viem, že cena za (x2) sa pohybuje okolo 1 000 až 1 500. Takže proste číselne to sedí.

Moja hľadaná hodnota bude:

8*320 + 8*1 280 =  2 560 + 10 240 = 12 800

Čo vy na to? :)