Matematické Fórum

To a.) a b.) som už počul no to ďalej nie a pre c.) Vychádzam z úvahy: 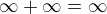a mám takéto riešenie: vys?ahujem tých čo tam sú, pomiešam s tými s autobusu a nas?ahujem. Môže by?? d.) obdobne.
hmmm... keďže by som podobne riešil aj e.), tak začínam ma? pocit, že to tak nebude.

↑ matoxy:

Potiz je jednak se zadanim prikladu, nebot stavajici hoste se stehuji jen v ramci hotelu, a nepujdou uz zpatky do autobusu. Jednak neni jasne, jak tyto lidi promicham s lidmi v autobusu, autobus je prece plny, stejne jako hotel. Ten vyraz oo + oo = oo nam v podstate rika, ze to nastehovani provest lze. Ukolem je vymyslet jak, tady najit zabydlovaci funkci (viz. ↑ sneakfast:)

Každému hostu přiřaďme číslo pokoje x, v němž daný host bydlí.

ad a) požádáme hosty, aby se přestěhovali do pokoje č. x+1. Tím pádem se uvolní pokoj č.1.
ad b) požádáme hosty, aby se přestěhovali do pokoje č. x+n. Tím pádem se uvolní pokoje č. 1, 2, ..., n.
ad c) požádáme hosty, aby se přestěhovali do pokoje č. 2x. Tím pádem se uvolní pokoje, jež jsou označeny lichými čísly. A těch bude nekonečně mnoho.
ad d) požádáme hosty, aby se přestěhovali do pokoje č. (n+1)x. Tím pádem se uvolní pokoje s čísly, jež po dělení číslem n+1 dává zbytek 1. Těch je nekonečně mnoho. Zde ubytuji 1. autobus. Dále se uvolní pokoje s čísly, jež po dělení číslem n+1 dává zbytek 2. Těch je také nekonečně mnoho. Zde ubytuji 2. autobus. Dále se uvolní pokoje s čísly, jež po dělení číslem n+1 dává zbytek 3. Těch je také nekonečně mnoho. Zde ubytuji 3. autobus. atd. Až nakonec n-tý autobus ubytuji do pokojů s čísly, jež po dělení číslem n+1 dává zbytek n. Těch je také nekonečně mnoho
ad e) požádáme hosty, aby se přestěhovali do pokoje 2^x ("^" znamená mocninu). Cestující z 1. autobusu ubytujeme do pokojů, jejichž čísla lze vyjádřit jako mocninu 3 (3,9,27,81,243,729,...). Cestující z 2. autobusu ubytujeme do pokojů, jejichž čísla lze vyjádřit jako mocninu 5 (5,25,125,625,3125,...). Cestující z 3. autobusu ubytujeme do pokojů, jejichž čísla lze vyjádřit jako mocninu 7 (7,49,343,...). Cestující ze 4. autobusu ubytujeme do pokojů, jejichž čísla lze vyjádřit jako mocninu 11 (11,121,1331,...) atd. Obecně, Cestující z n. autobusu ubytujeme do pokojů, jejichž čísla lze vyjádřit jako mocninu (n+1). prvočísla, které bereme z rostoucí posloupnosti všech prvočísel (2,3,5,7,11,13,17,19,atd.) Protože prvočísel je nekonečně mnoho, budou nakonec ubytování všichni cestující z vlaku a navíc nekonečně mnoho pokojů zůstane neobsazeno (pokoje, jejichž čísla lze vyjádřit jako součin alespoň dvou různých prvočísel).

d) Vyzve hosta z pokoje s číslem 1, aby se přestěhoval do pokoje s číslem 2. Host z pokoje s číslem 2 se přestěhuje do pokoje s číslem 4. Host z pokoje s číslem 3 se přestěhuje do pokoje s číslem 6, a tak dále. To znamená, že hosté budou nyní ubytováni v pokojích se sudými čísly. Potom všem novým hostům dá lichá čísla pokojů
 

e) Recepční přestěhuje všechny stávající hosty stejně jako v případu d) (hosté budou ubytováni s pokoji se sudými čísly). Nyní vagonům přidělí prvočísla počínaje číslem 3 (takže vagony budou mít čísla 3,5,7,11,13,… ∞).Každé sedadlo v každém vagonu rovněž očísluje čísly 1,2,3,… ∞. Každému novému hostu pak přidělí číslo pokoje, které dostane jako výsledek mocniny čísla vagonu umocněný číslem sedadla (tak např. noví hosté z vagonu s číslem 3 budou mít pokoje s čísly 3,9,27,81,… ∞, zvagonu s číslem 5 pak pokoje s čísly 5,25,125,625,.. ∞ atd.). Tím dostane jedinečná lichá čísla (prvočíslo (vyjma čísla 2) umocněné na libovolné přirozené číslo je opět liché číslo a toto číslo se neopakuje u žádného jiného umocněného prvočísla). Tak obsadí některé pokoje s lichými čísly.

Doplnil bych další úkol:

f) jak ubytovat nekonečně mnoho vlaků, který má nekonečně mnoho vagonů, kde v každém vagonu je nekonečně mnoho hostů? :-)

a šel bych dál - takovéto rozdělení na nekonečně mnoho částí bych provedl n-krát, takže by se jednalo o vlakovou soupravu skládající se z nekonečně mnoha podsouprav, označme je jako podsouprava 1. úrovně, každá z nich by obsahovala nekonečně mnoho dalších podsouprav (2.druhu) atd, až bych došel k podsoupravě (n-1). druhu. V každé z nich sedí nekonečně mnoho cestujících. Jak by vypadal předpis, který by tyto cestující ubytoval do Hilbertova hotelu tak, aby žádný pokoj nezůstal prázdný? :-)

Pokud poslední dvě otázky nejsou "soutěžní", tak bych si dovolil k nim něco napsat:

Vlak s 1+2+4+8+... cestujícími lze v pohodě ubytovat v každém běžném nekonečném hotelu.
Stačí když i-tého člověka z j-tého vagónu nastěhuju do patra 2^(j-1)+i.

K přeplnění standardního parkoviště však stačí, pokud na něj přijede jedna loď typu A (každá loď typu A má naloženy dvě lodě typu A) a pokusí se vyložit všechny lodě, které má naložené. Pokud by ale parkoviště mělo mocnost kontinua (tedy bylo by ve vesmíru, který není kvantovaný a lodě by byly hmotné body), pak by vyložení možné bylo.

Proč? Každé lodi přiřadím číslo. Vnější loď bude mít číslo 0.1. Lodě co jsou na ní 0.10 a 0.11. Lodě co jsou na první z nich budou 0.100 a 0.101, lodě na druhé 0.110 a 0.111, atd. Pokud se na tato desetinná čísla budeme dívat jako na dvojkové zápisy reálných čísel, pokryjeme takto celý interval (1/2,1). Ten má ale mocnost kontinua.

↑ Lishaak:

Ja myslim, ze problem je prave s tim binarnim zapisem. Je znamo, ze interval [0,1] je nespocetny. Tedy nelze usporadat vsechny prvky intervalu [0,1] do posloupnosti, coz Kondr provadi. Spor bychom jiste museli najit, nebot prave dukaz nespocetnosti intervalu [0,1] se provadi sporem (Cantoruv dukaz nespocetnosti intervalu [0,1]) a nejde se prece takovy prvek, ktery do takoveto posloupnosti nepatri. Ten dukaz je znamy sice v dekadicke podobe, ale to nema v tomto pripade zadny podstatny vyznam.

Je mozne ale, ze jsem to Kondrovo vysvetleni nepochopil. Uprimne receno, vrta mi to hlavou taky delsi dobu.

Jelikož je nějaký ten den po "soutěží", nastínil bych své řešení problému e) - "jak ubytovat vlak, ktery ma nekonecne mnoho vagonu, kde v kazdem vagonu je nekonecne mnoho hostu?"

Nech? uspořádaná dvojice označuje n-tého cestujícího v k-tém vagoně a uspořádaná dvojice hosta již ubytovaného v pokoji číslo n. Sestavme z těchto dvojic schéma:







Aby bylo možné všechny cestující ubytovat do Hilbertova hotelu, je třeba najít předpis, který bijektivně ubytuje každého cestujícího do příslušného pokoje resp. přestěhuje stávající hosty do jiných pokojů tak, aby po celé akci nezůstal v hotelu žádný pokoj volný. Hledejme bijekci

,

která "očísluje" uspořádané dvojice z horního schématu např. po diagonálách zprava doleva:





Najděme nejdříve obecný předpis, který zobrazuje uspořádané dvojice z prvního řádku prvního schématu na přirozená čísla z prvního řádku druhého schématu, tj.

g((0,1))=1, g((0,2))=2, g((0,3))=4, g((0,4))=7, g((0,5))=11 atd. Použitím funkce g modifikujeme  druhé schéma takto:






Využijeme-li faktu, že číslování probíhalo po diagonálách zprava doleva, pak není problém dokázat, že

Na uvedenou rovnost můžeme pohlížet jako na lineární diferenční(rekurentní) rovnici prvního řádu se speciální pravou stranou a počáteční podmínkou 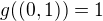. Vyřešením dostáváme návod, jak přesunout stávající hosty v Hilbertově hotelu a uvolnit tak místo pro příchozí cestující.





Pomocí tohoto řešení definujme g(n,k), pro , což je návod pro ubytování cestujících z vlaku, takto:


.