Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vypocet objemu ohraničeného plochami (TOTO TÉMA JE VYŘEŠENÉ)
#4 02. 06. 2014 15:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vypocet objemu ohraničeného plochami
199ado napsal(a):
tato podmínka mi nevyšla. Jak jsi počítal (já jsem hledala průsečíky a následně omezení v rovine xOy řešením rovnice  )? Děkuji.
)? Děkuji.
Offline
#6 02. 06. 2014 15:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vypocet objemu ohraničeného plochami
↑ 199ado: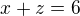 je rovina rovnoběžně ose y. Stopa této roviny v rovině xOy je přímka x=6, to je pravda, ale podstava útvaru, co počítáš, je průsečík 2 útvarů (takových neomezených "otevřených" válců nad parabolami
je rovina rovnoběžně ose y. Stopa této roviny v rovině xOy je přímka x=6, to je pravda, ale podstava útvaru, co počítáš, je průsečík 2 útvarů (takových neomezených "otevřených" válců nad parabolami  a
a  (to je jen část paraboly). tedy v podstavě je takový "lístek", nad kterým pokračuje válec. Potom ten válec je až v prostoru useknut rovinou
(to je jen část paraboly). tedy v podstavě je takový "lístek", nad kterým pokračuje válec. Potom ten válec je až v prostoru useknut rovinou 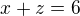 .
.
Zkus si to případně zakreslit ve WA.
Offline
#9 02. 06. 2014 16:50 Příspěvek uživatele zeus12 byl skryt uživatelem zeus12. Důvod: OMYL
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vypocet objemu ohraničeného plochami (TOTO TÉMA JE VYŘEŠENÉ)


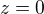

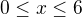

 ???
???