Matematické Fórum

Ahojte věnoval se někdo těm příkladum?Jde mi jen o pár bodu,abych měla zápočet,pomohl by mi někdo,kdyby byl zájem,zaplatila bych mu za to,potřebuji totiž ten přemět udělat.Děkuji mockrát

@Saturday: To nepomůže… Respektive nepomůže, když to naprogramuješ normálně. Zkus naprogramovat Bubblesort bez cyklů (jen pomocí rekurze) a bez pomocných proměnných (typicky na zachování hodnoty pole, když v bubblesortu prohazuješ dva prvky vedle sebe). Pak by se to mohlo přiblížit funkcionálnímu programování :-).

Já jsem se na to koukal a je to docela hardcore. Asi nad tím strávím víkend, jestli to chci udělat.

Ty metody třídění se dají najít na codecodexu. Ale nepředpokládám, že by z toho někdo něco extra pochopil, navíc tam používají fígle, které by asi Dostál neuznal (vnořený define, třeba).

zrejme neni, co zavidet :))

Já zkusím nadhodit myšlenku, jak naprogramovat ten Bubblesort. Procedura bude brát seznam a dál bude v sobě provádět dvě rekurzivní procedury (buď budou napsány mimo tuhle proceduru nebo pomocí pojmenovaných letů, to už je jedno).

V té vnitřnější proceduře provedeme tohle: čítač i nastavíme na 1 a dále porovnáme první prvek s druhým prvek a poté iterativně zavoláme tutéž proceduru s těmito parametry: čítač rekurze zvýšíme o jedničku (+ i 1) a dále vrátíme seřazený seznam (mensi-prvek vetsi-prvek). Teď porovnáváme dál. Porovnáme třetí prvek seznamu (určovat, který prvek zrovna porovnáváme s čím, bude čítač i) s největším prvkem v námi předaném seznamu (mensi-prvek vetsi-prvek), tedy s vetsi-prvek. Teď mohou nastat dva případy – třetí prvek je větší. To je ta jednodušší varianta. Poté iterativně zavoláme tutéž proceduru, kde pouze zvýšíme čítač o jedničku a na konec seřazeného seznamu přidáme ten třetí prvek, tedy předáme (mensi-prvek vetsi-prvek treti-prvek). Pokud je ovšem třetí prvek menší, musí ho uložit mezi hodnoty mensi-prvek a vetsi-prvek, což je o fous složitější. Tohle celé budeme opakovat tak dlouho, dokud neprojdeme celý seznam.

A ta vnější procedura bude dělat pouze to, že celý tenhle proces bude dělat (n – 1) krát, kde n je počet prvků v seznamu.

Determinant matice jde udělat tak, že si upravíš matici na trojúhelníkový tvar a determinant pak je součin prvků na hlavní diagonále. Asi by taky šlo postupovat podle klasické definice, to jsem ale nezkoušel: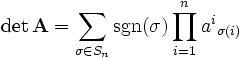



Inverzní matici už pak spočítáš jednoduše přes Adjungovanou matici.

Částečně ano – mám tam minimálně jednu chybu, kterou ještě musím nějak upravit.

Ahojky,nenapsal,by si mi aspon jeden příklad z těch matic prosímtě,jsem to zkoušela ale nešlo mi to,děkuji ti moc