Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 06. 2014 14:12
Inflexní body
Mám funkci  a potřebuji zjistit inflexní body. Udělal jsem druhou derivaci, položil proti nule a zjistil kořeny - inflexní body:
a potřebuji zjistit inflexní body. Udělal jsem druhou derivaci, položil proti nule a zjistil kořeny - inflexní body:
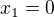

Ale podle wolframu je inflexní bod jen  http://www.wolframalpha.com/input/?i=in … 4%2F3%2B2x coz je videt i na grafu funkce. Proc? Diky
http://www.wolframalpha.com/input/?i=in … 4%2F3%2B2x coz je videt i na grafu funkce. Proc? Diky
Life in plastic, it's fantastic
Offline
- (téma jako vyřešené označil(a) Simon P40)
#2 06. 06. 2014 14:19 — Editoval kajzlik (06. 06. 2014 14:28)
Re: Inflexní body
Ahoj,
to, že má funkce nulovou druhou derivaci v bodě ještě neznamená, že ten bod je inflexní. Takový bod, kde je druhá derivace nulová, bývá též označován jako kritický.'"Nulovost" je podmínka nutná, ale nikoliv postačující.
Necháš-li si vykreslit graf té původní funkce, je to tam hezky vidět.
Je to podobné jako hledání extrému funkce  . Nula bude bod podezřelý z extrému, ale ověřením ( např. druhou derivací) zjistíš, že se v tomto bodě nachází sedlo.
. Nula bude bod podezřelý z extrému, ale ověřením ( např. druhou derivací) zjistíš, že se v tomto bodě nachází sedlo.
Offline
#4 06. 06. 2014 14:54
Re: Inflexní body
Pokud by ten bod inflexní byl, pak by na intervalech, které ti ten bod(y) vymezí, musela druhá derivace měnit znaménko.
Máš tedy subintervaly  . První dva mají záporné zn., třetí je kladný, tedy ve dvojce je inflexe.
. První dva mají záporné zn., třetí je kladný, tedy ve dvojce je inflexe.
Offline
