Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 06. 2014 16:35
Re: určitý integrál
↑ Simon P40:
Chybu jste udělal hned na začátku. Tvrdíte, že primitivní funkcí k 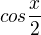 je
je  . Zkuste si tedy
. Zkuste si tedy  zderivovat a zjistíte, že to není pravda.
zderivovat a zjistíte, že to není pravda.
Offline
 jak se to spočítá?
jak se to spočítá?
![kopírovat do textarea $[ \sin \frac{x}{2}]_0^\pi$](/mathtex/00/00a6c0b4306d7721421ae13f25e8f96f.gif)

 (?) Kde mám chybu?
(?) Kde mám chybu?