Matematické Fórum

Simon P40 · 07. 06. 2014 13:12

Mohl by mi nkěkdo prosím vysvětlit princip grafického znázorňování funkcí, např.

$y>=x$
Umím nakreslit 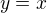$y=x$ , ale jak zjistím, která je to rovina pak?

nebo třeba $y>=x^2-1$ Taky umím nakreslit $y=x^2-1$ , ale nevím, jak logicky přijdu na to, která část bude vybarvená...
(dosazením bodů to trochu jde, ale není nějaké efektivnější řešení?)

Díky

Rumburak · 07. 06. 2014 14:04

↑ Simon P40:

Pomocí zápisů $y \ge x$ , $y \ge x^2-1$ a pod. nejsou popsány funkce, ale RELACE, což jsou obecnější útvary
než funkce.

Tak třeba rovnice $y=x^2-1$ určuje kvadratickou funkci, jejímž grafem je jistá parabola $p$ , zatímco nerovností
$y \ge x^2-1$ je - geometricky řečeno - určena možina bodů ležících nejen na prabole $p$ , ale i NAD touto parabolou.
(Ono "NAD" je míněno ve směru kladné orientace osy y , např. bod [1, 7] leží NAD bodem [1, 6].)

Simon P40 · 07. 06. 2014 15:42

chápu, díky

Matematické Fórum

#1 07. 06. 2014 13:12

graficky funkce

#2 07. 06. 2014 14:04

Re: graficky funkce

#3 07. 06. 2014 15:42

Re: graficky funkce

Zápatí