Matematické Fórum

Matej1117

Zdravim .. na tomto fore som nasiel odkaz na wikipediu, na ktorej je co to napisane o hyperkocke, docital som sa tam aj toto, citujem: "Medzi hyperkockou a kockou je vzťah ako medzi kockou a štvorcom."
Mozete mi niekto vysvetlit co tym bolo myslene? Hyperkocka ma velmi zaujima, kedze je to stvorrozmerna kocka a taku si neviem predctavit a pochybujem ze si ju niekto prectavit dokaze. Moze mat vlastnosti, na ktore ja neviem prist kdezto stvorec alebo kocka je lahko prectavitelna a vsetky vlastnosti mozem zistit sam. Dakujem.

gladiator01 · 11. 04. 2011 18:34

http://forum.matweb.cz/viewtopic.php?id=25086

OiBobik · 11. 04. 2011 18:48

↑ Matej1117:

(Někdo tvrdí, že si čtyřrozměrnou geometrii dokáže přímo představit a pracovat s ní, co je na tom pravdy, nevím, ani nevím, jak něco takového posoudit.)

Když ale potřebuješ pracovat s čtyřrozměrnou hyperkrychlí (jako hyperkrychle se myslím označují i krychle vícerozměrné), bývá většinou výhodné si ji představit jako dvojici krychlí, mezi které jsou spojeny dalšími hranami tak, že hrany mezi krychlemi představují jakoby isomorfismus mezi krychlemi (tedy nejlépe: namaluješ si dvě krychle vedle sebe, vrchol krychle A v přední stěně vlevo nahoře spojíš s vrcholem krychle B v přední stěně vlevo nahoře... atd.; někdy se to lépe znázorňuje "symetricky"); tyto nepřímé náhledy ti ovšem zprostředkují asi jen nějaké "nemetrické" vlastnosti.

Jinak ta poznámka o vztahu 4-rozměrné hyperkrychle, krychle a čtverce je myšlena tak, že se jedná o zobecnění krychle (nebo defakto čtverce: )) ), přičemž čtverec je 2 rozměrná hyperkrychle, krychle 3-rozměrná a tebou uvažovaná je 4-rozměrná hyperkrychle.

Matej1117

zaujimave diki za info .. a to je podla mna uplna blbost ze si ju niekto dokaze prectavit, ved ako si mozes prectavit stvorrozmernu kocku? Taka sa ani neda zostrojit, ved vsetky tri rozmery v obycajnej trojrozmernej kocke su na seba kolme, teda musis nejakym sposobom kolmo na tieto tri kolmice spustit dalsiu ale to sa neda. Skusal som si ju predctavit ale neviem no je to cudne urcite takato kocka neexistuje, iba matematicky mozno cisto teoreticky ale zostrojit sa neda.

OiBobik · 11. 04. 2011 19:25

↑ Matej1117:

To jo, zas na druhou stranu, jak chceš vyvrátit možnost toho, že to opravdu někdo dovede? : )) Do hlavy mu nevidíš. Mimochodem: Např. takový Kant by s tebou určitě (řekněme radši pravděpodobně) souhlasil. ; ))

Matej1117

Kant kto to je? a to ze niekomu do hlavy nevidim znamena ze nemaju dokaz ze si ju vedia prectavit, cize niekto to moze tvrdit ale nema to ako dokazat a zostrojit sa takato kocka neda, ten navod, ktory si mi dal ako ju zostrojit je sice pekny ale podla mna iba spojime dve kocky to nie je zas az taka veda a stale je to trojrozmerne teleso ale tak mozno ze to iba ja som taky obmedzeny a to nie je dobre :(

Ale tak ok dajmetomu ze existuje, potom ako sa vypocita objev, a povrch? A logicky - stvorec ma obvod a obsah, kocka ma objev a povrch, stvorrozmerna kocka ma tiez len objem a povrch alebo este nieco "tretie" ?? Mam pocit ze by mohla mat, je to cudny geometricky utvar ktory si ani neviem prectavit tak ma napada vselico .. A dalsia vec: Uhlopriecka stvorca je odmocnina s dvoch krat dlzka strany, uhlopriecka v kocke je odmocnina s trojky krat dlzka strany, hyperkocka bude mat podla mna odmocninu so styroch cise dva krat dlzka strany?? dobre rozmyslam?

gladiator01

↑ Matej1117:
Kant je německý filosof (nevim jestli myslel jeho)

Pavel Brožek · 11. 04. 2011 19:49

↑ Matej1117:

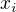Taková nejjednodušší hyperkrychle, jejíž jeden vrchol je v počátku, hrany mají délku 1 a jsou rovnoběžné s osami, je v podstatě množina bodů, které splňují $0\le x_i\le 1$ pro každé i od 1 do počtu dimenzí, kde $x_i$ je i-tá souřadnice.

Já si čtyřrozměrné objekty často předstauji tak, že čtvrtý rozměr nahradím časem. Takže třeba jednotkovou čtyřrozměrnou krychli si představuji takto:

Mám prázdný (trojrozměrný) prostor. V čase 0 se (z ničeho nic) objeví trojrozměrná krychle. V čase 1 zase zmizí.

Čtyřrozměrnou kouli o poloměru 1 zase takto:

Mám prázdný prostor. V čase -1 se objeví bod, který se okamžitě změní v malou kuličku. Ta se bude zvětšovat, v čase 0 bude mít poloměr 1 a pak se zase začne zmenšovat. V čase 1 se z ní stane bod a poté zmizí.

Kleinovu lahev:

Mám prázdný prostor. V něm si zvolím nějakou rovinu, ve které se bude odehrávat většina toho, co dál popíšu. V nějakém čase se v rovině objeví bod, který se okamžitě přemění v jednoduchou smyčku v té rovině. Ta se poté „zmáčkne“ tak, že se z ní v jednu chvíli stane osmička. Okamžitě poté se osmička rozpadne na dvě smyčky. Jedna smyčka se pak otočí kolem nějaké osy v rovině o 180° (pouze na toto otočení potřebuji třetí rozměr mimo rovinu). Po otočení jedné smyčky mám opět obě smyčky v rovině. Ty se po chvíli dotknou, vytvoří osmičku a ihned přejdou v jednu smyčku. Ta se bude smršťovat až do bodu, který poté zmizí.

Snad jsem to napsal správně :-)

Matej1117 · 11. 04. 2011 20:00

a my ludia aj vsetko ostatne sme v trojrozmernom priestore ne?

OiBobik · 11. 04. 2011 20:47

↑ Matej1117:

Otázka existence a neexistence věcí je taky svým způsobem příliš filosofická na to, aby měla jasnou odpověď : D Mohli bychom dokonce dojít k závěru, že neexistuje ani krychle nebo čtverec.

Ano, měl jsem na mysli onoho německého filosofa. On právě pracoval s pojmy jako je "forma názoru", která podle něj je společná všem lidem (dalo by se říci bytostem uvažujícím a myslícím v našich podmínkách) - tou je podle něj právě apriorní představa prostoru a času (v oné "přirozené" podobě - tedy prostor má tři rozměry, čas je něco kvalitativně odlišného - alespoň v naší mysli je, zřejmě si jej nepředstavujeme staticky jako ostatní rozměry, ale dynamicky - což je jenom opis toho, že si čas představujeme kvalitativně jinak : )) ). Ten by asi taky tvrdil, že čtyři rozměry si "staticky" nelze představit.

(Kanta ovšem znám jenom takto povšechně, nikoli nějak do podrobna, tak se předem omlouvám, jestli jej interpretuji nějak mylně - myslím však, že pro obecnou představu je to popis dostatečný a nepříliš zavádějící, těžko říct.)

Jinak ten můj návod není návod, jak čtyřrozměrnou krychli sestrojit, jak ty říkáš (ono je koneckonců otázka, co myslíš "sestrojit" - to je obvykle u dvourozměrných objektů přímé zobrazení, u trojrozměrných konstrukce nějakého průmětu do dvou rozměrů - přičemž určitě lze udělat něco jako průmět 4-roz. hyperkrychle do 3 rozměrů, do dvou potom taky, když od takového trojrozměrného průmětu narýsuješ dvourozměrný průmět - akorát tím postupně ztrácíš informace o samotném promítaném objektu), nýbrž jak si ji nepřímo představit, abys s ní mohl nějak pracovat (přičemž poznámka o "metrických vlastnostech" byla směřována právě na to, že na úvahy o objemu, obsahu se právě taková představa nehodí).

Matej1117 · 11. 04. 2011 20:52

tvoj prispevok ma nuti zamysliet sa nad viacerymi vecami takze momentalne ani neviem co mam nato odpisat :D

matweba · 12. 04. 2011 08:02

"Medzi hyperkockou a kockou je vzťah ako medzi kockou a štvorcom."
Když se čtverec umístí do 3D prostoru - objemu, pak lze z jeho vrcholu vést 3. úsečku - kolmici k předešlým.
Když se krychle umístí od 4D prostoru, pak lze z jejího rohu vést 4. úsečku - kolmici k předešlým.
Porovnání pro povrch hyperkrychle na:
odkaz 4D
Promítání do roviny jako převod z 4D prostoru do 2D prostoru.

SuchSoft

Tak ja som sa týmto trošku zaoberal a dopracoval som sa k vzorcu, pomocou ktorého sa dá vypočítať počet m-rozmerných podhyperkociek n-rozmernej hyperkocky. (Pod pojmom hyperkocka myslím hocijakú n-rozmernú kocku, aj 0-, 1-, 2- a 3-rozmernú)

Vzorec:
$(^{n}_{m})2^{n-m}$

Respektive po úprave:
$2^{n-m}\frac{n!}{(n-m)!\cdot m!}$

Takže ak chcem vypočítať koľko hrán (úsečiek) (1-rozmerné hyperkocky) má kocka (3-rozmerná hyperkocka), tak dosadím
$n=3$ a $m=1$ a vypočítam:
$2^{3-1}\frac{3!}{(3-1)!\cdot 1!}=2^{2}\frac{6}{2!\cdot 1} = 4\frac{6}{2}=4\cdot 3 = 12$

Platí: $m,n \in \mathbb{Z}$ a $m,n \ge 0$

dokonca to funguje aj pre $m>n$ - výsledkom bude 0.
No a možno by to mohlo platiť aj pre záporné čísla, len si neviem predstaviť záporné dimenzie.

Tento vzorec som vymyslel počas niekoľkých ciest trolejbusom do a z práce :)

Stretol sa niekto s niečím takýmto podobným? Ak poznáte niekto zaujímavý odkaz na internete alebo literatúru ohľadne tohto, dajte mi vedieť. Díky.

Ešte mi napadlo, doplním, že pomocou tohto vzorca sa dá dokázať, že každý rozmer musí byť ohraničený dvoma hranicami, napr. úsečka (n=1) dvoma bodmi (m=0), vo štvorci (n=2) štyrmi úsečkami (m=1), v kocke (n=3) šiestimi plochami (m=2) vo 4-rozmernej kocke (n=4) ôsmimi kockami (m=3), atď.

Takže dokázať sa to dá tak, že do vzorca dosadím $m=n-1$

vznikne:
$2^{n-(n-1)}\frac{n!}{(n-(n-1))!\cdot (n-1)!}=2^{n-n+1}\frac{n!}{(n-n+1)!\cdot (n-1)!}=$ $2^{1}\frac{n!}{1!\cdot (n-1)!}=2\frac{n(n-1)!}{(n-1)!}=2n$

Počet hraníc rozmerov (dimenzií) n-rozmernej hyperkocky je 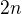$2n$
Čo znamená, že v n-rozmernej hyperkocke je každý rozmer (je ich n) ohraničený dvoma hraničnými (n-1)-rozmernými hyperkockami.