Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Spojitosť n-rozmernej "identity" v boxovej topológii (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 06. 2014 14:57
Spojitosť n-rozmernej "identity" v boxovej topológii
čaute pravdepodobne to bude zase jednoduché ,ale
existuje topologický priestor X ( samozrejme nediskrétny)
taký , že pre každú indexovú množinu I je funkcia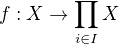
definovaná predpisom
spojitá pri boxovej topológii?
Boxová topológia je taká ktorej báza je tvorená produktami otvorených množín
zaujímavé sú najmä nekonečné indexové množiny lebo na konečných produktoch boxová topológia je to isté čo produktová topológia (generovaná vzormi projekcií teda najmenšia topológia pri ktorej sú projekcie spojité)
a pri produktovej topológii platí, že
je spojitá práve vtedy
keď všetky indexované gčka sú spojité
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 09. 06. 2014 13:55
Re: Spojitosť n-rozmernej "identity" v boxovej topológii
Napr.  s antidiskretnou topologiou
s antidiskretnou topologiou  . Ak ma byt aspon
. Ak ma byt aspon  tak musi byt diskretna.
tak musi byt diskretna.
Zvolme 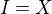 a
a 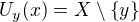 ak
ak 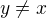 a
a 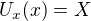 . Nech
. Nech 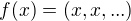 . Potom
. Potom 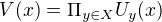 je otvorene okolie
je otvorene okolie  v box topologii. Teda ak ma byt
v box topologii. Teda ak ma byt  spojite, tak
spojite, tak 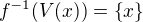 musi byt otvorena mnozina pre kazde
musi byt otvorena mnozina pre kazde  a teda topologia na
a teda topologia na  musi byt diskretna.
musi byt diskretna.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Spojitosť n-rozmernej "identity" v boxovej topológii (TOTO TÉMA JE VYŘEŠENÉ)
