Matematické Fórum

OndraVesely · 09. 06. 2014 20:31

Zdravím,

Mohli byste mi prosím vysvětlit jak se spočítalo to červeně podtržené?

//forum.matweb.cz/upload3/img/2014-06/38650_soucet.png

Nechápu proč se tam jako berou jen 3 členy k=1,2,3 pokud se to tak vubec udělalo. Jak se tam dostali ty zlomky $\frac{1}{n+1},\frac{1}{n+2},\frac{1}{n+3}$ ?

Jediné čemu snad rozumím je že ty členy, které mají to $n$ ve jmenovateli v limitě jdou k nule tak se potom vynechají

Děkuji

Andrejka3 · 09. 06. 2014 20:37

↑ OndraVesely:
Ahoj.
Jsem si jistá, že pokud si tu sumu rozepíšeš třeba od jedné do 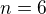$n=6$ , že Ti to dojde.

Andrejka3 · 10. 06. 2014 13:14

Přišel jsi na to?

OndrasV · 10. 06. 2014 13:24

↑ OndraVesely: Ondro, uvědom si, co je první člen, tj. pro k = 1, je to 1-1/4. Tj. to znamená, že ta první část členu posloupnosti $a_{k}=\frac{1}{k}-\frac{1}{(k+3)}$ se nepožerou pro k=1,2,3. Tj. proto je dílčí součet 1+1/2+1/3 + ... členy jdoucí k nule.

Matematické Fórum

#1 09. 06. 2014 20:31

Součet řady

#2 09. 06. 2014 20:37

Re: Součet řady

#3 10. 06. 2014 13:14

Re: Součet řady

#4 10. 06. 2014 13:24

Re: Součet řady

Zápatí