Matematické Fórum

bonifax

čau, potřeboval bych poradit, asi už blouzním, ale nijak nic nevidím, počítám příklad.
odstraním absolutní hodnotu dle postupu níže na konci obvykle udělám průnik, zde ale to vypadá, že je třeba sjednotit intervaly na konci, aby vyšel dobrý výsledek. Intervaly pro případy, kdy je x^2-17 kladný a záporný nemají žádné společné prvky, očekával bych prázdnou množinu, ale neni? žádný společný prvek tedy znamená sjednotit? ?VVV

$2^{|x^2-17|}>256$
$2^{|x^2-17|}>16^2$
$2^{|x^2-17|}>2^8$
$|x^2-17|>8$

$x^2-17>8$
$x^2>25$
$|x|>5$
$x\in (-\infty,-5)\cup (5,\infty )$

$-x^2+17>8$
$x^2<9$
$|x|<3$
$x\in (-3,3)$

Autor skryl část textu. Zobrazit/skrýt!

gadgetka · 10. 06. 2014 05:13

Mezi jednotlivými kořeny je slůvko "nebo", čili kořeny se na konci sjednocují. Pronikají se s definovanou množinou, kterou tys tady neuvažoval... Nulové body absolutní hodnoty jsou $-\sqrt{17}$ a $\sqrt{17}$ , ty rozdělí definiční obor na tři intervaly a pro ty řešíš nerovnici. Pro první interval vyjde $x\in (-\infty,-5)$ , pro druhý $x\in (-3,3)$ a pro třetí $x\in (5,\infty )$ . A tyto množiny se na konci sjednotí. :)

zdenek1 · 10. 06. 2014 07:14

↑ bonifax:
Malá rada. Tento typ je jednodušší řešit umocněním. Tím se zbavíš nutnosti rozdělovat to na jednotlivé intervaly.
$|x^2-17|>8$ protože obě strany nerovnice jsou nezáporné, můžeme bez obav umocnit.
$(x^2-17)^2>8^2$
$(x^2-17)^2-8^2>0$ a nyní podle $a^2-b^2$
$(x^2-17-8)(x^2-17+8)>0$
$(x-5)(x+5)(x-3)(x+3)>0$ a pokud ti nedělají problémy nerovnice v součinovém tvaru, tak máš okamžitě řešení.

bonifax

↑ gadgetka:

jj pěkně díky. tvůj postup jsem dlouho nedělal, je aspoň myslím teda po každý vždy stejný udělat 3x průnik s intervaly, pro který platí a na konci 3x sjednotit ? + Prázdná množina nastává v tvém postupu, kdyby vyšlo po průniku 3x prázdná množina , jindy ne že jo?

Abych ještě upřesnil, myslel jsem tohle. tady je příklad. Dle postupu tady na konci neudělám sjednocení, ale průnik na rozdíl od předchozího příkladu. Neuvědomil jsem si , že budu muset na konci toto rozlišovat...

↑ zdenek1:
Jo to je přesně pro mě, naprosto ideální jen jeden interval naraz, ovšem myslím, že není moc univerzální, kdyby kupř. na pravé straně bylo záporné číslo tak asi nic nebude.

$3^{|x^2-8|}<9$
$3^{|x^2-8|}<3^2$
$|x^2-8|<2$

$x^2-10<0$
$|x|<\sqrt{10}$
$x\in (-\sqrt{10},\sqrt{10})$

$-x^2+8<2$
$x^2-6>0$
$|x|>\sqrt{6}$
$x\in (-\infty,-\sqrt{6})\cup (\sqrt{6},\infty )$

Autor skryl část textu. Zobrazit/skrýt!

gadgetka

Zase děláš chybu. Nulové body jsou $-2\sqrt 2$ a $2\sqrt 2$ . Ty ti rozdělí definiční obor na tři intervaly:
$1.\enspace x\in (-\infty; -2\sqrt2\rangle$
Do absolutní hodnoty dosadíš např. -4. Vyjde kladná, proto:
$x^2-8<2$
$x^2-10<0$
$(x-\sqrt{10})(x+\sqrt 10)<0$
Nulové body jsou $-\sqrt{10}$ a $\sqrt{10}$
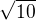
Do nerovnice dosadíš např. nulu, vyjde záporná, což my hledáme, nula se nachází mezi nulovými body, proto interval $(-\sqrt{10}; \sqrt{10})$ je řešením této nerovnice. To chápeš. Ale ty toto řešení pronikneš s definovanou množinou, čili:

$(-\infty; -2\sqrt2\rangle \cap (-\sqrt{10}; \sqrt{10})\Rightarrow x\in (-\sqrt{10}; -2\sqrt 2\rangle$

Stejně budeš postupovat při řešení dalších dvou intervalů:
$2. \enspace x\in \langle -2\sqrt 2; 2\sqrt 2\rangle$
$8-x^2<2$
dořešíš a kořen pronikneš s definovanou množinou

$3.\enspace x\in \langle 2\sqrt 2; \infty)$
$x^2-8<2$
opět dořešíš a uděláš průnik s definovanou množinou...

Na konci všechna tři řešení sjednotíš.

Postup Zdenka je daleko rychlejší, ale platí pro jednodušší nerovnice, kdybys měl více absolutních hodnot, tak toto řešení je jistota, jak sám jinými slovy píšeš... :)

gadgetka

A takhle vypadá sjednocení těch jednotlivých řešení:

//forum.matweb.cz/upload3/img/2014-06/99017_graf_950.png

Edit: V tvém skrytém řešení ti vypadlo mínus v prvním intervalu. :)

gadgetka · 10. 06. 2014 13:14

Umocněním je to fofr:
$(x^2-8)^2<4$
$(x^2-8)^2-2^2<0$
$(x^2-8-2)(x^2-8+2)<0$
$(x-\sqrt{10})(x+\sqrt{10})(x-\sqrt 6)(x+\sqrt 6)<0$
Nulové body:
$-\sqrt{10},\enspace -\sqrt 6, \enspace \sqrt 6, \enspace \sqrt{10}$

Do výrazu vlevo dosadíš např. nulu, abys zjistil, zda se chová kladně či záporně a označíš si na číselné ose plusy a mínusy:

//forum.matweb.cz/upload3/img/2014-06/98732_graf_951.png

Výraz vlevo má být menší než nula, proto vybíráš ty intervaly, ve kterých máš označeno mínus:
$K=(-\sqrt{10},-\sqrt{6})\cup (\sqrt{6},\sqrt{10})$

bonifax

↑ gadgetka:

Já tvému postupu rozumím , lze to klasicky přes tabulku :)..3 průniky 3x sjednotit ..tomu jsem se chtěl vyhnout, tak jsem našel jiný postup. Řeší se asi jako s jednou absolutní hodnotou, bez nutnosti ověřování, zda patří do příslušného intervalu. A na konci mají-li něco společné, potom se udělá průnik intervalů. Nemají-li intervaly nic společné, tak se sjednotí, kupodivu mi to ale také vychází stejně.. chyba tam dle mě nebude;)
u 1)
$5<|x|<3$ - nemají společné prvky => budeme sjednocovat.

$K=(-\infty ,-5)\cup (-3,3)\cup (5,\infty )$

u 2)
mají společné prvky => průnik
$\sqrt{10}>|x|>\sqrt{6}$

$K=(-\sqrt{10},-\sqrt{6})\cup (\sqrt{6},\sqrt{10})$

v jiném příkladě ozn. ho jako č. 3) ukážu, aby to bylo více jasné, proč myslím:) Je to obdoba mého postupu, jen se použije substituce, takže to vypadá čitelněji.

$5^{|x^2-6|}<125$
$5^{|x^2-6|}<5^3$
$|x^2-6|<3$
použiji substituci: $x^2=y$
$|y-6|<3$
$3<y<9$ - nahradím zpět x za y
$3<x^2<9$
$\sqrt{3}<|x|<3$
$K= (-3,-\sqrt{3})\cup (\sqrt{3},3)$

Postup příkladu 3) dle mého bez substituce: