Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Problemy se sumami (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 06. 2014 17:57 — Editoval OndraVesely (10. 06. 2014 18:03)
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Problemy se sumami
Dobry den, ucim se na test ze sum, narazil jsem na par nejasnosti. Doufam ze mi je pomuzete objasnit:
1] 
Mohli byste mi napsat jak se k tomu doslo? Potreboval vych vedet zdali je to nejaky vzorec pro zapamatovani nebo se to da odvodit.
2] 
Tady bych se chtel zeptat zdali toto mohu provest i pro ostatni pripady. Jaktoze lze toto provest?
3] 
Zde mi neni jasne proc jsme brali jen suda cisla a licha cisla jakoby vynechali
Dekuji
Offline
- (téma jako vyřešené označil(a) OndraVesely)
#3 10. 06. 2014 18:29
- OndraVesely

- Příspěvky: 71
- Škola: vysoká, 1. ročník
- Pozice: student
- Reputace: 0
Re: Problemy se sumami
↑ OndrasV:aha, ted uz je mi ta 2] jasna, to mam za to ze si nedelam peclive zapisy
Offline
#4 11. 06. 2014 06:42
Re: Problemy se sumami
↑ OndraVesely:
ad 1]
Pozorujme součet zlomků ve tvaru 1/k, kde hodnota k probíhá všechna přirozená čísla od 1 do 2n+1, kde n je nějaké přirozené číslo. Potom lze takový součet psát rozdělením na dva dílčí součty, např. s lichými jmenovateli a sudými jmenovateli. Odtud máme
Odtud plyne výsledek již snadno oddělením sčítance pro k=0 z poslední sumy a následnou úpravou do tvaru ve tvém dotazu.
ad 3]
Důkaz nebudu podrobně provádět, ale stačí si všimnout, že sčítance příslušející lichým indexům n jsou nulové, tedy stačí vzít pouze sudé. Korektně bychom měli postupovat analýzou parciálních součtů uvedené nekonečné řady.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Problemy se sumami (TOTO TÉMA JE VYŘEŠENÉ)
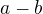 rozšíříš jedničkou ve tvaru
rozšíříš jedničkou ve tvaru  a dostaneš
a dostaneš  .
.