Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » pravdepodobnost vyberu dvou nesoudelnych cisel (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 06. 2014 17:43 — Editoval Andrejka3 (10. 06. 2014 18:14)
pravdepodobnost vyberu dvou nesoudelnych cisel
Ahoj. Prosím o pomoc s příkladem:
Pro dané  urči pravděpodobnost
urči pravděpodobnost  , že zvolíme-li náhodně dvě čísla
, že zvolíme-li náhodně dvě čísla  , budou nesoudělná. Ukaž, že
, budou nesoudělná. Ukaž, že
Spočítala jsem tohle:
Pro  označme
označme  , množinu všech prvočísel značme
, množinu všech prvočísel značme 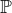 ,
,  .
.
Jsou  soudělná, právě když
soudělná, právě když  . Označme
. Označme  . Pak
. Pak
Podle principu inkluze a exkluze,
Nevím, jak dál.
edit: A pak ještě něco, ale vypadá to škareději (?) .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 10. 06. 2014 20:14 — Editoval vanok (10. 06. 2014 20:17)
Re: pravdepodobnost vyberu dvou nesoudelnych cisel
Ahoj
Toto si uz videla?
http://en.wikipedia.org/wiki/Coprime_integers
À toto?
Odkaz
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 10. 06. 2014 20:43 — Editoval Andrejka3 (10. 06. 2014 20:45)
Re: pravdepodobnost vyberu dvou nesoudelnych cisel
↑ vanok:
Ahoj.
Díky. Přečetla jsem si v prvním odkazu část Probablilities, a pochopila neformální důkaz (až na výpočet té limity, ale to mi nevadí).
Ohledně toho postupu, co jsem psala, doufala jsem, že snad nějaké tvrzení o dolních částech, nebo spíše pečlivé porovnání obou sum (zatím mi to připadá docela technické), by mohlo dát rovnost obou limit. Tak to asi bude v druhém odkazu, že.
edit: Akorát druhý odkaz jde stejnou cestou.
Il est clair que la probabilité qu'un nombre entier soit divisible par un nombre premier p est 1/p
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 10. 06. 2014 21:20
Re: pravdepodobnost vyberu dvou nesoudelnych cisel
↑ Andrejka3:, ten citat pokracuje.( Napr jedno zo 7mych je delitelne7mimy)
Potom probabilita aby dve cisla boli delitelne p, je 1/p^2, a proba aby aspon jeden nebol je 1-1/p^2.
Zvysok si rozumela?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 11. 06. 2014 07:41
Re: pravdepodobnost vyberu dvou nesoudelnych cisel
↑ vanok:
Ahoj, ano ten důkaz je pěkný, chci ale najít cestu od toho mého výpočtu k výsledku v odkazech. Snad se mi to povedlo :D : (1)
(1) (2)
(2)
Je  .
.
Takze  .
.
Z druhe strany  , kde
, kde .
.
Odtud,  .
.
Díky za pomoc.
What does a drowning number theorist say?
'log log log log ...'
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » pravdepodobnost vyberu dvou nesoudelnych cisel (TOTO TÉMA JE VYŘEŠENÉ)
