Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 06. 2014 16:48
Přijímačky MFF - bakalář
Tak dnes proběhl test na mff pro bakaláře... a jsem totálně v censored :D Připadá mi že příklady byly ještě těžší než 2012/13 :(
Zakroužkoval jsem 30/50 nakonec... ale jen 17 "na jistotu" (potřebujete 20 uznaných na postup), a jelikož vím jak to u mně s "na jistotu" vypadá... Ach jo taková škoda, informatiku jsem fajnšmekr mástr největší že jo a pak nezvládánu matiku u příjmaček. Na druhou stranu, naděje umírá poslední.
No nic tak ... jestli mně vezmou nebo ne, chtěl jsem se podělit o dva příklady co byly zajímavý IMO.
V algebrogramu představuje každé písmeno jednu číslici: 0, 1 ..., 9. Různým písmenům odpovídají různé číslice. V následujícím algebrogramu platí, že ani C ani E není nula.
(Sorry že to není v LaTeXu)
A x B = CA
+ - +
A x C = D
-------------
D x A = EC
Rozhodněte, která z následujících tvrzení o písmenech z tohoto algebrogramu platí:
(a) Číslice odpovídající písmenu C musí být menší než 5.
(b) Číslice odpovídající písmenům C a E musí být obě sudé.
(c) Číslice odpovídající písmenu B musí být rovna 6.
(d) Existuje více způsobů, jak lze přiřadit písmenům číslice, aby platily všechny rovnosti.
(e) Úloha nemá žádné řešení.
Co se týče mně tak jsem pojem algebrogram do dnes neznal :) Pochopil jsem to tak že ABCDE jsou číslice, a že rovnice jsou taky horizontálně, tzn. A+A=D; B-C=A; CA+D=EC; Z těch horizontálních mi ale vyšla kontradikce tak že jsem došel k závěru že to nemůže v žádném případě platit. Ale nebyl jsem si jist s těmi horizontálními znaky takže v konečných stresových 10 minutách jsem vyškrtal vše co nebylo E kdyby náhodou ABC(D) mohlo platit i zároveň. Ale tak, zajímavá úloha, co na to říkáte vy?
V krabičce na obrázku je každý ze tří vývodů (vstupů) vlevo propojen s jedním vývodem (výstupem) vpravo, každý vývod napravo je použit právě jednou. Možností jak za uvedených podmínek propojit vstupy a výstupy krabičky je celkem šest, jedna z nich je naznačena.
----------
-⊣-\/-⊢-
-⊣-/\-⊢-
-⊣----⊢-
----------
Nyní vezmeme tři krabičky stejného typu (označme ho T) a spojíme je za sebou: výstupy první napojíme na druhé, výstupy druhé na třetí.
--------- --------- --------
a1-⊣ ⊢--⊣ ⊢--⊣ ⊢-b1
a2-⊣ T ⊢--⊣ T ⊢--⊣ T ⊢-b2
a3-⊣ ⊢--⊣ ⊢--⊣ ⊢-b3
--------- --------- --------
(a) Pro každý typ T platí: vývodya
jsou spojeny.
(b) Pro alespoň čtyři typy T platí: vývodya
jsou spojeny.
(c) Pro každý typ T je spojenos
, nebo
s
, nebo
s
.
(d) Pro každý typ T platí: pro všechna i = 1,2,3 je spojenos
.
(e) Pro alespoň tři typy T platí: pro všechna i = 1,2,3 je spojenos
.
Co se týče mně tak tady jsem neskutečně zazmatkoval a ještě špatně přečet... V podstatě jednoduchá úloha, jenom trošku toho pochopení/"slovíčkaření". Škoda, 5 uznaných koleček navíc a cítil bych se mnohem líp. Snad pochopíte ten můj diagram :D
Offline
#2 11. 06. 2014 17:18
Re: Přijímačky MFF - bakalář
↑ a5438014:
Tak ten algebrogram....
Zjavne 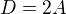 , takže z
, takže z 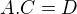 máme
máme  .
.
Potom 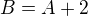 , takže
, takže 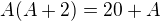 , z čoho
, z čoho  .
.
Takže  ,
,  a ľahko nájdeme
a ľahko nájdeme  .
.
Naozaj platí
4 x 6 = 24
+ - +
4 x 2 = 8
-------------
8 x 4 = 32
1^6 - 2^6 + 3^6 = 666
Offline
#3 11. 06. 2014 20:08
- antonijoker

- Zelenáč
- Příspěvky: 1
- Pozice: student
- Reputace: 1
Re: Přijímačky MFF - bakalář
Taky jsem delal prijimacky, bylo fakt hrozny. Snad tam dostanu. :( :)
Offline
#7 15. 06. 2014 23:59
Re: Přijímačky MFF - bakalář
což je ale samozřejmě dobře... člověk prokáže jistou dávku vynalézavosti
a o tom to je, ne všechno jde vyřešit podle předem známého algoritmu,
někdy si člověk ten algoritmus musí vytvořit sám :)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 17. 06. 2014 01:06
Re: Přijímačky MFF - bakalář
No příznám se, že mi připadne dost nesolidní při přijímacím testu na vš dávat témata, která nebyla probírána na sš.
A to proto, že test je časovaný a dost stresující a nevyřešení takovéhoto příkladu nedokazuje, že by člověk nebyl dostatečně talentovaný na obor.
Stalo se, že před započetím studia na jedné vš byli dva borci předem nadupaní na celý prvák, přitom ke konci fakulty vůbec nebyli nejlepší studenti hodnocením za všechny roky.
Offline
#10 17. 06. 2014 11:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Přijímačky MFF - bakalář
Zdravím,
↑ byk7: :-) někdo jde na informatika jen proto, že ho nevzali na AMU.
↑ Rumburak: na stránkách mají ukázky (zejména závěr zkoušky z ČJ je dobrý, kolegové zde tento problém také řešili).
↑ maver: to nemohu souhlasit - je to výběrové řízení a jasná kritéria. Talentovanost pro obor je ošetřena možností postoupit bez zkoušky (podmínky jsou zrovna dle talentu v oboru).
Stalo se, že před započetím studia na jedné vš byli dva borci předem nadupaní na celý prvák, přitom ke konci fakulty vůbec nebyli nejlepší studenti hodnocením za všechny roky.
To se obvykle vyvine - dost problému má ten, kdo si nezvykl připravovat jen z vlastního zájmu, ale jen na pokyn učitelů. Naopak - někomu vyhovuje nový systém (a sedí obor), tak problém nemá - na SŠ měl problémy s předměty, co "nesedí" nebo nepovažoval za podstatné.
Offline
#11 17. 06. 2014 13:13
Re: Přijímačky MFF - bakalář
↑ jelena:
Můj příspěvek je reakcí na číselné soustavy a binární operace na fit čvut (přitom v ukázkových testech z matematiky všech ostatních fakult čvut jsou zatím k tomuto datu plně dodržena témata sš matematiky).
Na příjimací testy a zkoušky během jakéhokoliv studia by měla být dodržována kritéria oznámení témat, ze kterých se bude zkoušet.
Jinými slovy, i jakýkoliv učitel může být nachytán při hodině, že neví to či ono ze svého oboru jenom díky tomu, že si jeho student nastuduje či zeptá na nějakou specifickou delikatesu. Vycházím z toho, že lidská bytost není stroj a nemá kapacity vědět všechno o všem.
Talent může student projevit u seminárek, diplomových prací, během studentské vědecké činnosti a možností zařadit se do fakultního výzkumu a publikovat již za studií. To, že si student načte nějaké téma navíc a náhodou se to "chytne" při nějakém testu nebo zkoušení není důkazem jeho matematického talentu, ale pouze zájmem o obor či tendenci hromadit encyklopedické informace, což je v dnešní době díky dostupnosti znalostních databází a internetu nepotřebné.
PS: Někdy to, že je student horší na sš a lepší na vš, může být i tím, že na sš neměl vhodné domácí prostředí (viz rušná rodina).
Offline
#12 17. 06. 2014 14:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Přijímačky MFF - bakalář
↑ maver:
nejsem organizátor žádného přijímacího řízení, ale každá fakulta vystavuje podmínky s předstihem, také je možné si upřesnit dotazem na organizátory. FIT umožňuje uznat výsledky NSZ z matematiky (znáte podmínky?) a až další možnost jsou vlastní testy FIT.
číselné soustavy a binární operace
jsou i u přijímacích testů na 8leté gymnázium (po 5. třídě ZŠ), jen se tomu tak neříká, ale testuje se schopnost zorientovat (samozřejmě, musí být také příprava). Na druhou stranu - v celém spektru testu "netradičně formulovaných úloh" bylo minimum.
Vy máte dojem, že je problém se dostat na zvolený obor (nemyslím na konkrétní fakultu, obor můžete kvalitně vystudovat i na jiné fakultě, než FIT)?
může být i tím, že na sš neměl vhodné domácí prostředí (viz rušná rodina).
určitě - vliv rodinného prostředí je klíčový, o tom bych žádnou polemiku nevedla.
Offline
#13 17. 06. 2014 17:26
Re: Přijímačky MFF - bakalář
Smrt offtopicu!! :D
Poslušně hlásím že nejsem totální kretén a přijímačky jsem prošel se 44 body ze sta! A to jsem byl už smířenej s tím že tam nepůjdu, už chápu proč je lepší být pesimista! :D No vida, každý den je školní den co? :D
Offline