Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 06. 2014 19:33
Re: Hledání všech komplexních čísel
Ahoj ↑ 1vecera:,
můžeš to řešit mechanicky - tj. vyřešit jednu rovnici (viz binomická rovnice) a zjistit jestli existují řešení, která vyhovují i druhé rovnici.
Lze to ale udělat mnohem snadněji. Jestliže ty rovnice, co jsi napsal, platí pro nějaká 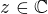 , pak pro tato
, pak pro tato  jistě platí i tyto rovnice:
jistě platí i tyto rovnice: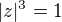
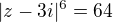
(vlastně jsem porovnal abs. hodnoty levých a pravých stran). Potom, protože abs. hodnota je nezáporná, platí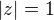
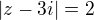
To jsou rovnice kružnic v komplexní rovině. Snadno nahlédneme, že mají jediný společný bod (dotyku), a sice  . Ovšem řešení
. Ovšem řešení 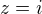 nesplňuje první zadanou rovnici (
nesplňuje první zadanou rovnici (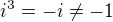 ). Z uvedeného plyne, že zadané rovnice nemají v
). Z uvedeného plyne, že zadané rovnice nemají v  řešení.
řešení.
Offline