Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 06. 2014 12:39 — Editoval Integral123 (27. 06. 2014 12:39)
- Integral123
- Příspěvky: 146
- Reputace: 2
Integral
Ahojte, studujem na strednej skole a brali sme iba derivacie a limity, tie viem ale pytal som aj ucitela a vraj integraly nebudeme brat co je mi luto, strasne moc by som chcel pochopit co to je. Ked som sa pytal oco tam ide tak mi povedal ze ide o pocitanie obsahu plochy pod nejakou useckou, ktoru reprezentuje nejaka funckia alebo tak nejako. Tak som si doma nacrtol jednoduchu funkciu  a skusal som sa nad tym zamysliet, po chvili som zistil ze plocha pod tou useckou je nekonecna ale ak pracujeme len na nejakom konkretnom intervale napr.
a skusal som sa nad tym zamysliet, po chvili som zistil ze plocha pod tou useckou je nekonecna ale ak pracujeme len na nejakom konkretnom intervale napr.  tak plocha ma konecny obsah, konkretne som zistil ze je to
tak plocha ma konecny obsah, konkretne som zistil ze je to  pre tuto funkciu. Chcem sa opytat, dostal som sa blizko ku integralu alebo som vedla?
pre tuto funkciu. Chcem sa opytat, dostal som sa blizko ku integralu alebo som vedla?
Offline
#2 27. 06. 2014 12:58
Re: Integral
Ahoj, super. Zkus stejným myšlenkovým postupem najít integrál pro konstantní funkci. Jsi na začátku cesty k Riemanovu integrálu (klikni pro odkaz na wiki).
Jinak, v druhém kole zkus najít integrál k všelijakým funkcím co Tě napadnou, když Ti řeknu, že výsledek integrálu po derivaci Ti má dát to, co integruješ. Neboli, jestliže jsi našel k funkci  integrál
integrál  , tak ten po zderivování dá zase zpátky "x":
, tak ten po zderivování dá zase zpátky "x": 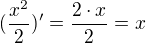 .
.
100*0>0 aneb stokrát nic umořilo osla
Offline
#3 27. 06. 2014 13:00 — Editoval Integral123 (27. 06. 2014 13:02)
- Integral123
- Příspěvky: 146
- Reputace: 2
Re: Integral
konstantnu funkciu? to by slo, to je mozno este lahsie ako toto co som napisal.. ja tie pojmy neovladam, ked som sa pozeral na ten znak integralu take predlzene "S" tak hore bolo cislo a dole bolo cislo na tych koncoch, to tiez neviem co je, ten riemanov integral vyzera dost jednoducho, aj tam pisu ze je to najjednoduchsi tip integralu
Offline
#4 27. 06. 2014 13:03 — Editoval Sherlock (27. 06. 2014 13:04)
Re: Integral
Ano, plocha pod křivkou nebo nad křivkou (když je záporná) funkce  na intervalu
na intervalu  se spočítá jako:
se spočítá jako:![kopírovat do textarea $\int_{a}^{b}f(x)dx=[F(x)]^{b}_{a}=F(b)-F(a)$](/mathtex/a5/a52c7edddf3c250eb3d3f455a13ef6ea.gif)
Kde  je primitivní funkce k funkci
je primitivní funkce k funkci  a platí
a platí 
Předpokládáme že funkce je na  buďto jenom kladná nebo jenom záporná. Kdyby se její hodnota na tomto intervalu střídala, bylo by potřeba to rozdělit na víc integrálů.
buďto jenom kladná nebo jenom záporná. Kdyby se její hodnota na tomto intervalu střídala, bylo by potřeba to rozdělit na víc integrálů.
Dále si prostuduj odkaz.
Offline
#5 27. 06. 2014 13:11
- Integral123
- Příspěvky: 146
- Reputace: 2
Re: Integral
ok idem si to prestudovat a inac je to tazke na pochopenie tato problematiku integralu? chcel by som sa to naucit aj take komplikovanejsie neskor
Offline
#6 27. 06. 2014 13:48 — Editoval Sherlock (27. 06. 2014 13:48)
Re: Integral
↑ Integral123:
Co se úvodu do integrálního počtu týče - těžký mi to rozhodně nepřišlo (v matematice je spousta horších věcí :-) )
Jenom to chce trochu cviku, co se konkrétních metod týče (per partes, substituce atd.)
Offline
#7 27. 06. 2014 14:11
Re: Integral
↑ Integral123:
Nejdříve se zkus podívat třeba Sem (to je určitý integrál - opravdu obsah plochy od osy x po křivku y=f(x) pro x v intervalu x=<a,b>)
A ještě jedna malá poznámka:
Jak v odkazu zjistíš, tak se tam sčítají plochy-obdélníky jejichž rozměry jsou vlastně délka=dx a výška=f(x) což je vlastně hodnota funkce v každém "x" bodu dělení. A když se dx bude blížit 0, tj. budeš to rozdělení zjemňovat, tak ten součet přejde na integrál (určitý).
On totiž symbol pro integrál je takový trochu znetvořený symbol pro sumu.
V tom odkazu co ti poslal↑ Sherlock: jsou už základní vzorečky pro výpočet neurčitého integrálu
Offline
#8 27. 06. 2014 18:15 — Editoval Rumburak (27. 06. 2014 18:18)
Re: Integral
↑ Integral123:
Ahoj.
K pochopení tzv. určitého integrélu je, myslím, užitečné zamyslet se nad následujjící situací:
Mějme na intervalu  definovánu spojitou (a "ne příliš zvrhlou") funkci
definovánu spojitou (a "ne příliš zvrhlou") funkci  nabývající pouze
nabývající pouze
kladných hodnot. Zvolme pevně  . Pro libovolné
. Pro libovolné  vznikne obrazec
vznikne obrazec  ohraničený
ohraničený
čtveřicí následujících křivek (dopručuji nákres):
- úsečkou odpovídající intervalu  na ose
na ose  ,
,
- obloukem křivky o rovnici 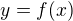 nad intervalem
nad intervalem  ,
,
- úsečkou z přímky o rovnici  určenou podmínkou
určenou podmínkou  ,
,
- úsečkou z přímky o rovnici  určenou podmínkou
určenou podmínkou  .
.
Je přirozené očekávat, že obrazec  bude mít nějaký plošný obsah - jeho neznámou číselnou hodnotu
bude mít nějaký plošný obsah - jeho neznámou číselnou hodnotu
označme  . Tuto funkci
. Tuto funkci  proměnné
proměnné  sice ještě definovánu nemáme, nicméně máme
sice ještě definovánu nemáme, nicméně máme
o ní určité představy dané přirozenou geometrickou intuicí. Konkretně: když 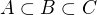 , kde
, kde 
jsou obdélníky a  je "rozumný" obrazec, potom očekáváme, že jeho obsah bude roven alespoň obsahu
je "rozumný" obrazec, potom očekáváme, že jeho obsah bude roven alespoň obsahu
odélníka  , ale nejvýše obsahu obdélnía
, ale nejvýše obsahu obdélnía  . Pomocí těchto představ a na základě definice derivace není
. Pomocí těchto představ a na základě definice derivace není
těžké zjistit, že pokud výše uvažované funkce  existuje, pak v každém bodě
existuje, pak v každém bodě  splňuje rovnici
splňuje rovnici  . Tento výsledek vede přímo ke vzorci
. Tento výsledek vede přímo ke vzorci
![kopírovat do textarea $\int_{a}^{b}f(x)dx=[F(x)]^{b}_{a}=F(b)-F(a)$](/mathtex/a5/a52c7edddf3c250eb3d3f455a13ef6ea.gif) ,
,
o němž se zmínil Sherlock a který je základem Newtonovy definice integrálu, při jiných definicích integrálu se
pak dokazuje jako věta - zpravidla pro funkci  spojitou na daném intervalu . (Definic určitého integrálu je
spojitou na daném intervalu . (Definic určitého integrálu je
více - od různých autorů, každá z nich má své výhody i nevýhody, ale to není téma pro začátečníka.)
Offline
#9 27. 06. 2014 20:49
#10 29. 06. 2014 11:12 — Editoval Integral123 (29. 06. 2014 11:32)
- Integral123
- Příspěvky: 146
- Reputace: 2
Re: Integral
prestudoval som si to PDFko a mam otazku - co je to primitivna funkcia? to mi trochu nie je jasne preco ju hladame a co to je, to mi je najmenej jasne z tych vsetkych pojmov.
Offline
#11 30. 06. 2014 09:47 — Editoval Rumburak (30. 06. 2014 09:48)
Re: Integral
↑ Integral123:
Jestliže na některém intervalu  je funkce
je funkce  derivací funkce
derivací funkce  (tj.
(tj.  pro libovolné
pro libovolné  ),
),
potom ekvivalentně říkáme, že na intervalu  je funkce
je funkce  primitivní funkcí k funkci
primitivní funkcí k funkci  . Proč při výpočtu
. Proč při výpočtu
obsahu plochy "pod" křivkou o rovnici 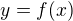 hledáme primitivní funkci k
hledáme primitivní funkci k  , jsem se snažil vysvětlit ve svém
, jsem se snažil vysvětlit ve svém
příspěvku ↑ Rumburak: . Zaměř svoji pozornost tam a když Ti něco z toho nebude jasné, tak se klidně zeptej.
Offline
#12 10. 07. 2014 11:44 — Editoval Integral123 (10. 07. 2014 11:44)
- Integral123
- Příspěvky: 146
- Reputace: 2
Re: Integral
myslim ze uz som pochopil preco je pojem primitivna funkcia taky dolezity .. dakujem
Offline
