Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 07. 2014 16:49 — Editoval Secren (16. 07. 2014 16:53)
Podiel vlastných derivácii
Zdravím,
mam jednu nejasnosť v dôkaze tejto vety --> 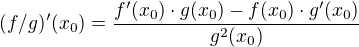
pre 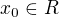 a
a 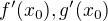 su vlastne
su vlastne
Tu je samotny dokaz a cast ktora mi nie je jasna.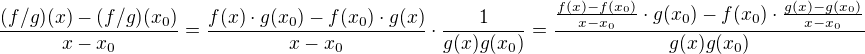
Uprava z toho 2. vyrazu na 3. mi nie je jasna. (dalej to dokoncit nie je problem len tu nevidim preco sa to rovna). Resp. ak sa nemylim preco piseme za  >>>
>>> 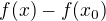 a potom to iste g(x).
a potom to iste g(x).
Offline
- (téma jako vyřešené označil(a) Secren)

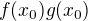 , tj.
, tj.![kopírovat do textarea $f(x) g(x_0) - f(x_0) g(x) = [f(x) g(x_0) -f(x_0) g(x_0)] + [f(x_0) g(x_0) - f(x_0) g(x)] = \cdots$](/mathtex/27/279b189ab4115f60fd8a473d8bb902a9.gif)
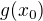 a
a 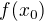 před hranaté závorky.
před hranaté závorky.