Matematické Fórum

pietro · 16. 07. 2014 11:52

Ahojte !
Pekné letko prajem.

Vedeli by ste prosím popísať túto "dvojkrivku" v priestore
napr. parametrickou rovnicou?

x=f1(t)
y=f2(t)
z=f3(t)

pričom platí y=ax^2 +bx+c

//forum.matweb.cz/upload3/img/2014-07/04302_kvadraticka.GIF

Nákres som videl aj tu:

http://digitalcommons.unl.edu/cgi/viewc … hmidexppap

Ďakujem a pozdravujem :-)

Rumburak

↑ pietro:
Ahoj.

Nevím, zda se ztrefím do toho, co potřebuješ.

Nechť $V = [u, v, w]$ je společný vrchol těch parabol. Ta "horní" bude v souřadnicovém systému Pxyi
popsána soustavou

$y = A(x-u)^2 + w , i = 0 , (A > 0)$ ,

ta "dolní" soustavou

$y = B(i-v)^2 + w , x = u , (B < 0)$ .

Odtud bych vyšel. Odpoleledne snad zkusím popojít o krůček dál.

EDIT: Opravena chyba v poslední soustavě rovnic.

pietro · 16. 07. 2014 15:27

↑ Rumburak:Ďakujem za Tvoje pripojenie k téme. Priznám sa, že tápem. Chcem si len urobiť nejakú geometrickú predstavu o imaginárnej jednotke. A myslím, že keď túto dvojkrivku vyjadríme čo najelegantnejšie možno sa rozjasní.A keby si mal na túto tému iné poznatky, pripoj ich prosím.
Taktiež riešenie, koreňov kvadratickej rovnice pomocou diskriminantu či je len jediné vo vesmíre:-) tak ako sme sa to učili.

Rumburak · 16. 07. 2014 16:10

↑ pietro:

Chcem si len urobiť nejakú geometrickú predstavu o imaginárnej jednotke.

Snad to téma nakonec nějak doladíme, ale zatím se moc nechytám, pokud jde o to, co hledáš.

A keby si mal na túto tému iné poznatky, pripoj ich prosím.

Napdlo mě, že by Tě mohly zajímat kvaterniony.

pietro · 16. 07. 2014 17:48 — Editoval pietro (16. 07. 2014 18:17)

↑ Rumburak:
možné paramatrizovanie by bolo aj ( podľa Tvojho naštartovania, niečo som síce drobne upravil)

horná krivka
$x_{h}=t_{h}$
$y_{h}=A(t_{h}-u)^{2}+v$
$z_{h}=w$

dolná

$x_{d}=u$
$y_{d}=-A(t_{d}-w)^{2}+v$
$z_{d}=t_{d}$
dal som rovnaké A, komplexné korene to asi "žiadajú", a teraz to ešte overiť v nejakom peknom 3d grafe
zatiaľ len tento mám Odkaz

ale je to také voľajaké symetrické....

Rumburak

↑ pietro:

Ještě doplním pár informací (potřeboval jsem si je v klidu rozmyslet) .

Jak určitě víš, tak teorie komplexních čísel rozvíjí

- algebru (třebas pokud jde o řešitelnost algebraických rovnic) ,

- anylýzu (dává do souvislosti goniometrické funkce s exponenciálními, nabízí hlubší vhled do rozvojů funkcí
v mocninné řady, poskytuje důležité metody pro výpočet některých typů integrálů a pro řešení diferenciálních
rovnic, ...) .

Mimo to teorie komplexních čísel může plnit i funkci analytické geometrie roviny:

Komplexní číslo v algebraickém tvaru $z = x + y\,\mathrm{i}$ koresponduje s bodem $[x , y]$ případně vektorem $(x , y)$
eukleidovské roviny opatřené kartéskou soustavou souřadnic $Pxy$ , při tom

- absolutní hodnota k.č. odpovídá velikosti vektoru,

- součet dvou k.č. odpovídá součtu dvou vektorů ,

- součin k.č. a reélného č. koresponduje s reálným násobkem vektoru ,

- křivku o rovnici $f(x,y) = 0$ můžeme pomocí jazyka k.č. zapsat ve tvaru $f(\Re z, \Im z) = 0$

atd.

Navíc součin dvou k.č. nám poskytuje elegantní způsob, jak vyjádřit operaci otočení o daný úhel okolo
daného středu (viz Moivreova věta).

Z těchto příkladů je vidět, že k.č. jsou velmi geometrická, a to ve smyslu Eukleidovské geometrie roviny.
Pokud by Ti toto nepomohlo, tak zkus přesněji napsat, jaké geometrické vlastnosti imaginární jednotky
Tě zajímají.

pietro · 20. 07. 2014 11:56

↑ Rumburak: Pozdravujem :-)

Čoraz viac sa mi javí, že $i$ by som si nemal predstavovať ako "číslo" kvantifikovateľné , ale ako operátor.

1. Najprv sa riešili problémy so zápornými číslami, pri príkladoch typu menej mínus viac ... ?= 5-7
V týchto lineárnych úlohách ( kde figurovalo len $x^{1}$ ) "pomohlo" zavedenie mínus jednotky (mj),
predpis $(mj)^{1}=-1$ .

Slovný popis operácie : to čo vyjde v príklade menej mínus viac, sa rovná tomu istému, ako viac mínus menej, ale opatrené s nejakým novým znakom, trebárs mínusom.
$5-7=7-5= 2*mj= -2$
Operátor "zámeny" vačšieho za menšie).

2. No a v oblasti , kde figurujú kvadratické členy $x^{2}$ sa tiež "trápenie" zo zápornej odmocniny odstránilo
tak isto zámenou
$\sqrt{(5-7)}=\sqrt{(7-5)i^{2}}=i\sqrt{2}$
predpis imag.jednotky bol tentoraz v kvadratickej oblasti
$i^{2}=-1$

No a ešte, keď sa "dá" aplikovať maticový počet na vyjadrenie komplexných čísel, tak sa mi javí imaginárna jednotka ešte bližšie k operáciám.

Rumburak

↑ pietro:

Ahoj.

Čoraz viac sa mi javí, že $i$ by som si nemal predstavovať ako "číslo" kvantifikovateľné , ale ako operátor.

Komplexní čísla mají podle mne jednak svoji "pasivní" roli bodů v rovině, jednak "aktivní" roli operárorů v rovině.
Např. operace $z \mapsto \mathrm{i} z$ představuje otočení bodu $z$ o pravý úhel okolo středu v bodě 0 a můžeme pak vnímat
$\mathrm{i}$ jako symbol pro tuto operaci.
Podobně i vektor v geometrii je de facto operátorem - zajišťujícím operaci posunutí. Místo $X+\vec{u}$ bychom mohli
psát $\vec{u}(X)$ . Rovněž tato role vektoru přechází na komplexní čísla, takže např. zmíněná imaginární jednotka
má dvě "operátorské" role, podle toho, zda s ní dané kompl. číslo $z$ vynásobíme nebo sečteme.

Holt komplexní čísla jsou poněkud abstraktní struktura, do níž na rozdíl od čísel reálných nelze rozumným způsobem
zavést uspořádání, což je, myslím, hlavní příčina, proč nelze imaginární čísla dobře "kvantifikovat". Lámat si s tím
hlavu není potřeba, berme to, jak to je definováno - v matematice se studují i mnohé ještě abstraktnější struktury.
Hrajeme-li třeba šachy, také jednotlivá pravidla hry nesrovnávíme s "praktickými" představami o možných situacich
na reálném bojišti. I k matematice je dobré přistupovat jako k jakési hře - s pojmy a symboly podle vymezených
pravidel.

pietro · 22. 07. 2014 17:28

↑ Rumburak:

Ahoj.

Ďakujem za Tvoju trpezlivosť a cenné reakcie. Dávajú mi v mojej obmedzenej pozorovanej dimenzii predsa len akési objasnenie.

Rád by som si však v 3 rozmernom euklidovskom priestore ( ktorý je myslím najbližší model nášho optického vnímania skutočnosti) aspoň naznačil, kde sa komplexné korene skrývajú. Ten obrázok vyššie mi niečo napovedá.

Ale principiálne, rád by som aj vyriešil korene kvadratickej rovnice čisto len prostriedkami AG ( keď už je aká taká názorná predstava na obrázku vyššie).

Brano · 22. 07. 2014 18:22 — Editoval Brano (22. 07. 2014 18:27)

Ak si chces (komplexne) riesenie kvadratickej rovnice vizualizovat tak mozes napr. aj takto

Mas $at^2+bt+c=0$ aby to bolo netrivialne, tak mame $a\not=0$ ale potom mozme rovnicu predelit $a$ a dostaneme $t^2+2pt+q$ ale aby sme si to este zjednodusili tak si posunme stred, t.j. uvazujme $z=t+p$ (nie je to nutne kvoli obrazku ale lahsie sa mi bude pisat) - dostaneme
$z^2+r=0$
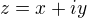kde $f=z^2+r$ je komplexna funkcia komplexnej premennej $z=x+iy$ , tak uvazujme
$\text{Re }f=x^2-y^2+r$ a $\text{Im }f=2xy$ teda ak ma byt $f=0$ potom
$x^2-y^2+r=0$ co je hyperbola, ktoru si lahko nakreslis a
$xy=0$ co je kuzelosecka pozostavajuca z dvoch (osovych) priamok
Prienikom tychto kuzeloseciek su vo vseobecnosti dva body.

PS: Lahko si mozes nakreslit aj situaciu s neposunutym stredom a z obrazka aj hned bude vidiet preco pre rovnicu s realnymi koeficientami musia byt komplexne korene zdruzene.
PPS: Takto si to mozes kreslit aj pre rovnicu s komplexnymi koeficientami.

pietro · 23. 07. 2014 10:00 — Editoval pietro (01. 08. 2014 08:33)

↑ Brano: Ďakujem Ti pekne, naštudujem a už idem maľovať :-)

Len doplním ešte predošlé

//forum.matweb.cz/upload3/img/2014-08/74796_04302_kvadraticka.GIF

pietro · 02. 08. 2014 10:53

Našiel som celkom príjemnú grafickú stránku.

Autor skryl část textu. Zobrazit/skrýt!

Matematické Fórum

#1 16. 07. 2014 11:52

Korene kvadratickej rovnice

#2 16. 07. 2014 12:23 — Editoval Rumburak (17. 07. 2014 12:14)

Re: Korene kvadratickej rovnice

#3 16. 07. 2014 15:27

Re: Korene kvadratickej rovnice

#4 16. 07. 2014 16:10

Re: Korene kvadratickej rovnice

#5 16. 07. 2014 17:48 — Editoval pietro (16. 07. 2014 18:17)

Re: Korene kvadratickej rovnice

#6 17. 07. 2014 09:49 — Editoval Rumburak (18. 07. 2014 10:36)

Re: Korene kvadratickej rovnice

#7 20. 07. 2014 11:56

Re: Korene kvadratickej rovnice

#8 21. 07. 2014 10:17 — Editoval Rumburak (21. 07. 2014 11:34)

Re: Korene kvadratickej rovnice

#9 22. 07. 2014 17:28

Re: Korene kvadratickej rovnice

#10 22. 07. 2014 18:22 — Editoval Brano (22. 07. 2014 18:27)

Re: Korene kvadratickej rovnice

#11 23. 07. 2014 10:00 — Editoval pietro (01. 08. 2014 08:33)

Re: Korene kvadratickej rovnice

#12 02. 08. 2014 10:53

Re: Korene kvadratickej rovnice

Zápatí