Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 02. 2009 21:03 — Editoval matoxy (18. 02. 2009 21:19)
Exponenciálna rovnica
Zdravím,
mal by som taký problém v škole sme dostali rátali (a nedorátali) takýto príklad: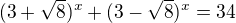 .
.
Napadlo ma to riešiť rozkladom oboch ľavých zátvoriek pomocou binomickej vety a keďže je v druhej zátvorke pre sqrt8 mínu po sčítaní rozkladov nám vypadnú všetky členy kde bude sqrt8 umocnené na nepárny exponent. Potom sa dopátrame ku riešeniu rovnice x=2, ale len tak že si skúsime dosadiť dva a sedí to. To by sme však v podstate mohli robiť už hneď aj bez rozkladu. Okrem toho malo výsť aj x_2=-2 a to mi nevychádza. Ako by sa to malo riešiť?
Editace: čosi ušlo:)
You know who
(or maybe not)
Offline
#4 18. 02. 2009 21:36 — Editoval lukaszh (18. 02. 2009 21:41)
Re: Exponenciálna rovnica
↑ matoxy:
A čo takýto prevod: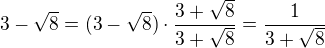
Potom sa ti rovnica pomerne jednoducho prevedie na tvar: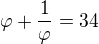
po substitúcii 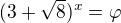
Inak k tej binomickej vete. Ak predpokladáš, že 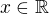 , tak treba používať zovšeobecnenú binomickú vetu. Tá klasická stredoškolská je pre prirodzené čísla.
, tak treba používať zovšeobecnenú binomickú vetu. Tá klasická stredoškolská je pre prirodzené čísla.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#5 19. 02. 2009 06:48
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Exponenciálna rovnica
↑ matoxy:
Opravdu podle postupu ↑ lukaszh: už jednoduchou úpravou vyjde 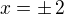
Nikdo není dokonalý
Offline
#11 19. 02. 2009 12:38 — Editoval Cheop (19. 02. 2009 12:38)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Exponenciálna rovnica
↑ musixx:
Ano máš naprostou pravdu jde to tedy ještě upravit,
ale v době moderních kalkulaček já už nic neupravuji a
pokud mě vyjde logaritmus, tak to hned házím do stroje.
PS: Jinak moc hezká úprava.
Nikdo není dokonalý
Offline
#12 19. 02. 2009 13:06
Re: Exponenciálna rovnica
↑ Cheop: Jiste, kalkulacce se samozrejme vubec nebranim. Ale kdyz kalkulacka ukaze vysledek, ktery bude "pravdepodobne" hezky, tak stoji zato si dokazat, ze se napriklad zadna desetinna mista neschovala za jeji zobrazitelnost. Ostatne tady jsem vicemene vysledek z kalkulacky vyuzil (ne pouzil), protoze jak by me jinak melo napadnout, ze se mam zrovna divat na druhou a minus druhou mocninu z cisla  ? ... Ale jo, mohlo by me to napadnout, treba se v
? ... Ale jo, mohlo by me to napadnout, treba se v  divat na mocniny
divat na mocniny  a zkoumat, kdy to bude
a zkoumat, kdy to bude  , ale o to v teto uloze preci nejde, to je jasne. :-)
, ale o to v teto uloze preci nejde, to je jasne. :-)
Offline

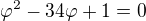 . Z toho
. Z toho 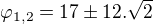 .
. . Tu 2 a -2 sedí, ale ako k tomu prídeme?
. Tu 2 a -2 sedí, ale ako k tomu prídeme?
 . To už iba pomocou kalkulačky alebo sa tam dá ešte nejaká úprava?
. To už iba pomocou kalkulačky alebo sa tam dá ešte nejaká úprava?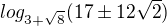 a "duverovat jen kalkulacce". Samozrejme si s tim jde pohrat.
a "duverovat jen kalkulacce". Samozrejme si s tim jde pohrat.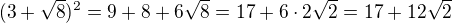 a
a  , a proto plati:
, a proto plati: