Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 08. 2014 10:15
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
konvergencia taylorovho radu
Ahoj.
Potreboval by som skontrolovať môj postup.
V príklade ide o to, aby som k danej fukncii f našiel jej taylorov rozvoj a určil či konverguje ku funkcii + polomer konvergencie. , kde
, kde  a
a  .
.
Taylorov rozvoj funkcie f v bode b rádu n je: , kde výraz
, kde výraz  je definovaný nasledovne:
je definovaný nasledovne:
j=0 => 1
j=1 => k
j=2 => k(k+1)
j=3 => k(k+1)(k+2) etc.
Ku zisteniu či tento rozvoj pre 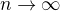 konverguje ku f, musím ukázať, že pre zvyšok (volím lagrangeov tvar) platí:
konverguje ku f, musím ukázať, že pre zvyšok (volím lagrangeov tvar) platí: , pre theta z (1,2).
, pre theta z (1,2).
Teda môžem vyhodiť z tej limity konštanty, konkrétne  .
.
Dostanem  .
.
Ďalej si zadefinujem j-ty čiastočný súčet  . Ak ukážem, že tieto čiastočné súčty konvergujú pre nejaké x, potom to musí znamenať pre tú limitu, že pre tieto x je nulová.
. Ak ukážem, že tieto čiastočné súčty konvergujú pre nejaké x, potom to musí znamenať pre tú limitu, že pre tieto x je nulová.
Preznačme,  , potom
, potom  a podielovým kritériom dostaneme:
a podielovým kritériom dostaneme: .
.
Pre konvergenciu: -1<z<1, 
 .
.
Tzn., že existuje okolie bodu b, kde to konverguje, a teda ta limita je na tom okolí nulová.
Keďže bod b bol ľubovoľný, tak to platí pre všetky  .
.
Záver, postupnosť čiastočných súčtov taylorovho rozvoja funkcie f v bode b konverguje pre  .
.
Je to správne? Ďakujem.
Offline