Matematické Fórum

Brzls · 18. 08. 2014 18:27 — Editoval Brzls (18. 08. 2014 18:51)

Zdravím

Neumím dokázat, popřípadě vyvrátit, jestli platí tato věta.

Mějme diferencovatelnou funkci f(x) definovanou pro všechna reálná čísla. Pokud existují limity v plus i mínus nekonečnu, tak $\lim_{x\to\infty }\frac{df}{dx}(x)=\lim_{x\to-\infty }\frac{df}{dx}(x)=0$

Je to pravda či nikoli? Já jen vycházím z intuitivního pohledu a náčrtku, ani nevim jak bych důkaz začal...

Edit: zkoušel jsem to přes Lagrangeovu větu o střední hodnotě, ale akorát jsem se dopracoval k tomu, že existuje posloupnost a(n) taková, že lim f'(a(n))=0 ale nějak to dotáhnout z toho se mi už nedaří

Eratosthenes

ahoj ↑ Brzls:,

pravda to není. Např. pro f(x)=x^2 je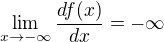

$\lim_{x\to -\infty }\frac{df(x)}{dx}=-\infty$

$\lim_{x\to\infty }\frac{df(x)}{dx}=\infty$

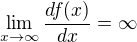
Pro f(x) = sin x limity neexistují.

Atd.

Bati · 18. 08. 2014 20:03 — Editoval Bati (18. 08. 2014 20:20)

Ahoj.
↑ Eratosthenes:
Brzls měl existencí limit na mysli pravděpodobně jejich konečnost.

↑ Brzls:
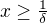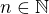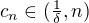Když není hned vidět jak a zdá se ti, že tvrzení bude platit, zkus to sporem, např. ať $f'(+\infty+)=:L>0$ . Z definice limity hned plyne, že existuje $\delta>0$ takové, že $f'(x)>\tfrac L2$ pro všechny $x\geq\tfrac1{\delta}$ . Teď můžeme použít tu Lagrangeovu větu: vezmeme $n\in\mathbb{N}$ , splňující $n>\tfrac1\delta$ a dostáváme existenci bodu $c_n\in(\tfrac1{\delta},n)$ takového, že $f(n)-f(\tfrac1{\delta})=f'(c_n)(n-\tfrac1{\delta})>\tfrac{L}2(n-\tfrac1{\delta})$ . 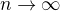Pro $n\to\infty$ tedy nutně 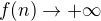$f(n)\to+\infty$ , což je spor. Zbývá udělat případ, kdy 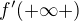$f'(+\infty+)$ neexistuje. Edit: a tento případ ve skutečnosti nastat může, vezmi např. funkci $\frac{\sin{x^2}}{x}$ . Takže tvrzení neplatí ani s konečnými limitami.

Brzls · 19. 08. 2014 01:12

[re]p437966|Bati[/
Ano dotaz by ta mysleny. Ted uz si i dokazu predstavit jak by vypadala funkce pro kterou to neplati. Zkusim aspon vymyslet a dokazat za jakych silnejsich predpokladu to plati. Dekuji za odpoved

Bati · 19. 08. 2014 10:54

↑ Brzls:
No ta část důkazu, kterou jsem uvedl dokazuje tvrzení za dodatečného předpokladu, že $f'(+\infty+)$ existuje.
Možná bych se ještě zamyslel nad tím, jak to dopadne pokud ta funkce bude monotónní.

Matematické Fórum

#1 18. 08. 2014 18:27 — Editoval Brzls (18. 08. 2014 18:51)

Důkaz věty

#2 18. 08. 2014 19:23 — Editoval Eratosthenes (18. 08. 2014 19:24)

Re: Důkaz věty

#3 18. 08. 2014 20:03 — Editoval Bati (18. 08. 2014 20:20)

Re: Důkaz věty

#4 19. 08. 2014 01:12

Re: Důkaz věty

#5 19. 08. 2014 10:54

Re: Důkaz věty

Zápatí