Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » komplexní analýza - konformní zobrazení, lineární lomená transformace
#1 09. 08. 2014 10:50
komplexní analýza - konformní zobrazení, lineární lomená transformace
Ahoj, potřebovala bych pomoct s postupem v následujících dvou příkladech:
1.
Užitím konformního zobrazení  najděte řešení
najděte řešení  následující okrajové úlohy
následující okrajové úlohy pro
pro  ,
, pro
pro  ,
, pro
pro  ,
,
kde  ,
, ,
, .
.
Načrtněte několik vrstevnic nalezeného řešení  . (Za omegama mají být množinové závorky, nevím, proč se nezobrazují.)
. (Za omegama mají být množinové závorky, nevím, proč se nezobrazují.)
2.
Užitím lineární lomené transformace najděte řešení  následující okrajové úlohy
následující okrajové úlohy pro
pro  ,
, pro
pro  ,
, pro
pro  ,
,
kde  ,
, ,
, .
.
Načrtněte několik vrstevnic nalezeného řešení  . (Za omegama mají být množinové závorky, nevím, proč se nezobrazují.)
. (Za omegama mají být množinové závorky, nevím, proč se nezobrazují.)
Děkuji za reakce!
Offline
#2 16. 08. 2014 13:07
Re: komplexní analýza - konformní zobrazení, lineární lomená transformace
tak k 1)
riesenie rovnice  je v podstate ekvivalentne tomu, ze hladas holomorfnu funkciu v tvare
je v podstate ekvivalentne tomu, ze hladas holomorfnu funkciu v tvare  kde
kde  splna pozadovane okrajove podmioenky.
splna pozadovane okrajove podmioenky.
O  platia taketo pekne veci. a) je to holomorfna transformacia b) je to zlozenie kruznicovej inverzie (jednotkovej kruznice) a zrkadlenia okolo realnej osi, takze sa lahko nahliadne, ze
platia taketo pekne veci. a) je to holomorfna transformacia b) je to zlozenie kruznicovej inverzie (jednotkovej kruznice) a zrkadlenia okolo realnej osi, takze sa lahko nahliadne, ze  t.j. zvisla priamka cez bod
t.j. zvisla priamka cez bod  a
a  je zvisla priamka cez bod
je zvisla priamka cez bod  .
.
Teda hladas  v tvare
v tvare  kde
kde  je holomorfna na pasiku medzi tymi priamkami a splna dane okrajove podmienky, inymi slovami ak
je holomorfna na pasiku medzi tymi priamkami a splna dane okrajove podmienky, inymi slovami ak  tak riesis
tak riesis  s tym, ze
s tym, ze  a
a  - co sa aj lahko uhadne, lebo rieseniami Poissonovej rovnice su napr. linearne funkcie a tie lahko nasijes na dane okrajove pomienky t.j. dostanes
- co sa aj lahko uhadne, lebo rieseniami Poissonovej rovnice su napr. linearne funkcie a tie lahko nasijes na dane okrajove pomienky t.j. dostanes  . To mozes teraz dosadit do Cauchy-Riemannovych vztahov a dostanes
. To mozes teraz dosadit do Cauchy-Riemannovych vztahov a dostanes  cize ked to potom spojis, tak mas
cize ked to potom spojis, tak mas  , C je lubovolna realna konstanta.
, C je lubovolna realna konstanta.
Cize potom mas  a teda
a teda  .
.
v 2) tak podobne - treba si nakreslit tie hranice a zistis, ze kroznicova inverzia s kruznicou v strede  a polomerom jedna by bola fajn a tak uvazuj
a polomerom jedna by bola fajn a tak uvazuj  .
.
Offline
#3 22. 08. 2014 08:12
Re: komplexní analýza - konformní zobrazení, lineární lomená transformace
↑ Brano: Ahoj, promin, ze reaguju az ted, spadlo mi to do spamu... Mohl bys mi prosim pomoct s tou kruhovou inverzi? Jak si ji mam predstavit? Konkretne jak se kruznice o polomeru 1 se stredem v -1 zmeni na primku prochazejici bodem -1/2?
Offline
#4 22. 08. 2014 16:32 — Editoval Brano (22. 08. 2014 18:48)
Re: komplexní analýza - konformní zobrazení, lineární lomená transformace
nejake zakladne info najdes tu: http://en.wikipedia.org/wiki/Inversive_ … _inversion
v podstate ide o to, ze mas nejaku fixovanu kruznicu ktora urcuje zobrazenie z roviny do roviny, co sa vola inverzia - pravidla ako sa to robi najdes v tom odkaze. Inverzia sa to vola preto, lebo zobrazi vnutro kruhu na vonkajsok a naopak.
Je to ale pomerne pekne zobrazenie, lebo
1) je inverzne samo sebe, t.j. ked ho zlozis so sebou mas identitu
2) zobrazuje kruznice-alebo-priamky na kruznice-alebo-priamky.
3) ta definicna kruznica pozostava z bodov co sa zobrazia samy na seba
4) stred inverzie zobrazi na "bod nekonecno"
teda kuznicu prechadzajucu stredom inverzie zobrazi na priamku a ked chces zistit aku, tak staci najst nejake dva body ktore na nej musia byt - co v tom pripade na ktory sa pytas je jednoduche, lebo mozes zobrat tie body prieniku - tie musia ostat zachovane
no a v komplexnych cislach sa s nou robi jednoducho: inverzia voci kruznici so stredom v 0 a polomerom 1 ma predpis  ak chces trebars stred
ak chces trebars stred 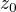 a polomer
a polomer  tak sa to da vyskladat z tejto zakladnej inverzie a posuvania a skalovania - konkretne to je
tak sa to da vyskladat z tejto zakladnej inverzie a posuvania a skalovania - konkretne to je 
cize funkcia  je zlozenie invezie a komplexneho zdruzenia, co je iba zrkadlenie voci realnej osi.
je zlozenie invezie a komplexneho zdruzenia, co je iba zrkadlenie voci realnej osi.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » komplexní analýza - konformní zobrazení, lineární lomená transformace

