Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 08. 2014 23:01
- paja.ppp

- Příspěvky: 101
Postačující podmínka konvergence.
Dobrý den,
ráda bych se zeptala jaká je postačující podmínka pro konvergenci řad.
Nutná podmínka- s limitou částečného součtu neplatí například u harmonické řady (a ještě u dalších?) a to mě mate, protože jsme si a doteď uváděli tuto podmínku jako jedinou a bohužel to nikde ani nemohu dohledat.
Předem děkuji za odpovědi.
Vznáší se letí
vzduch lehce brázdě
odvážný mladý muž
na létající hrazdě…
Offline
#2 25. 08. 2014 00:54
Re: Postačující podmínka konvergence.
↑ paja.ppp:
Zdravím.
Konvergence řady je (v nejjednodušším případě) definována jako konvergence posloupnosti jejích částečných součtů, a proto jsou tyto pojmy ekvivalentní.
Nutná podmínka pro konvergenci určité řady je to, že její členy konvergují k nule.
Vlastnosti harmonické řady jsou důkazem toho, že předchozí podmínka není postačující.
Postačující podmínka pro konvergenci řady  je např.
je např.  pro všechna
pro všechna 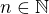 , anebo prostě
, anebo prostě  .
.
Offline
