Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 26. 08. 2014 20:41 — Editoval misaH (26. 08. 2014 20:54)
- misaH
- Příspěvky: 13460
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
.
Skús si dať ten kosínus do kalkulačky. Jeden aj druhý.
Nemáš to dobre "premenené".
Offline
#3 26. 08. 2014 20:49
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
Ale kdyz se podivam jasne do tabulky zde:
http://www.e-matematika.cz/stredni-skol … kci-01.jpg
tak je tam jasne napsano ze pro 3pi/4 je to zaporne a sinus kladny
Offline
#5 26. 08. 2014 20:55 — Editoval misaH (26. 08. 2014 21:53)
- misaH
- Příspěvky: 13460
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
Že to nemajú byť 
 je kladný
je kladný
Offline
#7 26. 08. 2014 21:31 — Editoval bonifax (26. 08. 2014 22:04)
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
Ahoj ↑ Prdonek44:
řekl bych, že chyba je v tom, že, když odečítáš periodu 2pí, tak nemůžeš dál odčítat periodu, pokud úhel je už zobrazitelný na jednotkové kružnici. V tomhle případě již úhel  se vejde do jednotkové kružnice.
se vejde do jednotkové kružnice.
Pozn 1) Já dělal na VŠE letos 2x již v červnu. Přeji hodně štěstí, třeba se jednou potkáme ve škole.
Pozn 2) Používáš-li tabulku vzorců doporučuji používat tu, co dostaneš u přijímaček. Ta se může lišit od té, co si našel na netu.
http://kmat.vse.cz/wp-content/uploads/2 … uprava.pdf
edit: oprava)
koukám, že jsem přeskočil periodu, díky ↑ misaH:
Offline
#8 26. 08. 2014 21:50
- misaH
- Příspěvky: 13460
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
No neviem teda.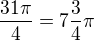
6 pi ide dole, zostane 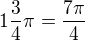
I V. kvadrant, kosínus kladný, sinus záporný.
Zaujíma nás znamienko kosínusu.
Offline
#9 26. 08. 2014 22:56
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ bonifax:
Tak dekuji nejak jsem to vymyslel s tim odecitavanim -2pi a fungovalo to u peti prikladu tak snad. Jinak ja uz taky delal prijimacky na finance, ale ucil jsem se 2 dny a jeste k tomu jsem dostal variantu s kombinatorikou :D. Takze ve ctvrtek to snad napisu a dostanu se na FIS a nebudu muset na cvut :)
Offline
#10 27. 08. 2014 11:58
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
Jeste bych se chtel zeptat tady: http://materialy.rubesz.cz/prijimaci_zkousky/vse-11-d0/ u prikladu 12
vyjde sinx/2=0 ktere se v zadanem intervalu vyskytuje 3x a to x1=0,x2=pi,x3=2pi. Pak jeste druhy koren ktery se vyskytuje jednou. Celkem tedy 4 reseni ovsem priklad ma mit 3 reseni.
Offline
#11 27. 08. 2014 12:33 — Editoval Cheop (27. 08. 2014 12:33)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
Právě řešení: to jsou tedy v intervalu <0;2pi> 2 řešení nikoliv 3 řešení
to jsou tedy v intervalu <0;2pi> 2 řešení nikoliv 3 řešení
Nikdo není dokonalý
Offline
#12 27. 08. 2014 13:19
- marnes

- Příspěvky: 11227
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
Zkusím ještě jinak.
Když se převádí na základní úhel -  tak od zadaného kladné úhlu odečítáme úhel plný
tak od zadaného kladné úhlu odečítáme úhel plný 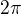
Když je tedy zadán úhel ve čtvrtinách, tak plný úhel je  (kdyby v sedminách, tak
(kdyby v sedminách, tak 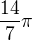 atd)
atd)
pak 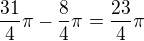 to ale není stále úhel základní, pokračuji tedy dál
to ale není stále úhel základní, pokračuji tedy dál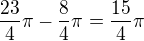 stále není
stále není a to je úhel základní
a to je úhel základní
dá se to urychlit tak, že si říkáme násobky čísla 8 - 8;16;24;32, ale 32 už je více než zadaných 31 a proto odečteme jen 24 
tak třeba pomůže
Jo. A na začátku vás zdravím.
Offline
#13 27. 08. 2014 13:26 — Editoval marnes (27. 08. 2014 13:27)
- marnes

- Příspěvky: 11227
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
K druhému příkladu je potřeba si uvědomit, či nakreslit (použít třeba nabízené programy), že když je tam argument funkce  , tak pro graf to znamená, že se "natáhne" do dvojnásobné velikosti.
, tak pro graf to znamená, že se "natáhne" do dvojnásobné velikosti.
Takže když byl u  první průsečík v
první průsečík v 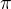 , tak u
, tak u  bude ve dvojnásobné vzdálenosti, tedy
bude ve dvojnásobné vzdálenosti, tedy 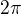 a mezi tím nic
a mezi tím nic
Jo. A na začátku vás zdravím.
Offline
#15 27. 08. 2014 13:58
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
Když vidím jak válčíš s úhly, možná by bylo lepší si to místo Moivreovy věty napsat jako 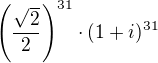 a závorku potom upravit postupně
a závorku potom upravit postupně 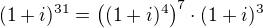 . Jednoduchým roznásobením se dá zjistit, že
. Jednoduchým roznásobením se dá zjistit, že  a
a 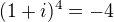 . A pak je to už jednoduché. Tím neříkám, že budoucí student VŠ nemá ovládat látku ZŠ, ale pokud něco neumím, je lepší si vybrat bezpečnější způsob, byť je delší. Tak to jen abys věděl, že Moivreova věta není jediný způsob.
. A pak je to už jednoduché. Tím neříkám, že budoucí student VŠ nemá ovládat látku ZŠ, ale pokud něco neumím, je lepší si vybrat bezpečnější způsob, byť je delší. Tak to jen abys věděl, že Moivreova věta není jediný způsob.
ČVUT bych nebral jako záchranu ("nebudu muset"), tam se přece jen nějaká práce vyžaduje, stejně jako znalost látky ze ZŠ a SŠ (ačkoli se to nekontroluje přijímačkami). I když na některých fakultách je tragédů pravda taky dost.
Offline
#16 27. 08. 2014 20:51
- marnes

- Příspěvky: 11227
Re: Imaginarni/realna cast komplexniho cisla je rocna cislu
↑ Prdonek44:
Pokud jde o 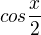 tak ano
tak ano
Jo. A na začátku vás zdravím.
Offline
