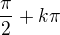Matematické Fórum

Vaclav · 15. 02. 2009 21:05

Ahoj, může mi někdo prosím poradit jak dostanu toto?

(R+r) * cos (a) * cos (b) - (R+r) * sin (a) * sin (b) = (R+r) * cos (a+b)

a toto?

(R+r) * cos (a) * sin (b) + (R+r) * sin (a) * cos (b) = (R+r) * sin (a+b)

Děkuji Venca

kaja.marik · 15. 02. 2009 21:15

rika se tomu souctove vzorce

jendula11 · 15. 02. 2009 21:17

↑ Vaclav:
zacni treba tim ze vytknes R+r

halogan · 15. 02. 2009 21:18

To jsou součtové vzorce pro goniometrické funkce

$\sin (a + b) = \sin a \cdot \cos b + \sin b \cdot \cos a \nl \sin (a - b) = \sin a \cdot \cos b - \sin b \cdot \cos a \nl \nl \cos (a + b) = \cos a \cdot \cos b - \sin a \cdot \sin b \nl \cos (a - b) = \cos a \cdot \cos b + \sin a \cdot \sin b \nl$

Vaclav · 15. 02. 2009 21:22

Jasné, jsem pako.
Dík za osvěžení paměti.

teniska · 20. 02. 2009 13:15

prosim pomuze mi nekdo s timto prikladem? (1/(sin(x)^2)) je to hrozne moc dulezite..budu vdecna

jendula11 · 20. 02. 2009 13:36

↑ teniska:nějak mi uchází pointa co máš na mysli že by se s tím dalo dělat?

jendula11 · 20. 02. 2009 13:39

jediné co mě napadá $1+cotg^2x=\frac{1}{sin^2x}$

teniska · 22. 02. 2009 15:07

↑ jendula11: no prubeh funkce...

jendula11 · 22. 02. 2009 19:25

no průběh fce to je trošku abstraktní pojem co přesně neumíš ?

teniska · 22. 02. 2009 20:43

↑ jendula11: nevim co mam delat kdyz prvni derivaci polozim nule..tak nevim kolik je x?

O.o · 22. 02. 2009 20:53

↑ teniska:

Položíš ji rovnu nule a zjistíš pro jaká x je derivace rovna nule. Rovnou sem svůj pokus zkus napsat, oki? ;)

jendula11 · 22. 02. 2009 20:59

první derivace mi vyšla $\frac{-2cos(x)}{sin^3(x)}$
prvni derivace rovna nule v $\frac{\pi}{2}+k\pi$
snad se nepletu

teniska · 22. 02. 2009 21:23

↑ jendula11: dekuju moc :-) a ma tahle funkce asymptoty??

jendula11 · 22. 02. 2009 21:26

to nevím skus si určit v krajních bodech def. oboru a pak se směrnicí

teniska · 22. 02. 2009 21:29

↑ jendula11: aha takze mam spatne kdyz mi def.obor vysel vsechny real. cisla,??

jendula11 · 22. 02. 2009 21:31

to každopádně v předpisu funkce vidím zlomek a mě už od malička učili že nulou nejde dělit

teniska · 22. 02. 2009 21:33

↑ jendula11: :-D aha..takze vsechny real.cisla krom nuly nebo krom K pí ?a limita bez smernice bude teda lim x jdouci k nule?

jendula11

všechna reálná čísla kromě K pi, v tom už je zahrnuta i ta nula když je K=0

teniska · 22. 02. 2009 21:41

jj dekuji...möc mi to pomohlo...:-) a jeste jestli muzu mit jeden stupidni dotaz do sinusu nejde dosadit nekonecno ze?:-)

jendula11 · 22. 02. 2009 21:44

nevím jak je to přesně myšleno ale nekonečno se nikam nedosazuje to není nějaké konkrétní číslo.

teniska · 22. 02. 2009 21:47

↑ jendula11: myslela sem jak je limita se smernici tak jde k nekonecnu...ale to uz neres hrozne moc dekuji mam alespon neco ahoj:-)

jendula11 · 22. 02. 2009 21:48

↑ teniska:
tak u limity to jo ale tam se nedosazuje tam pouze zjištuješ hodnoty blízké danému bodu, nemáš zač

Matematické Fórum

#1 15. 02. 2009 21:05

goniometrické funkce

#2 15. 02. 2009 21:15

Re: goniometrické funkce

#3 15. 02. 2009 21:17

Re: goniometrické funkce

#4 15. 02. 2009 21:18

Re: goniometrické funkce

#5 15. 02. 2009 21:22

Re: goniometrické funkce

#6 20. 02. 2009 13:15

Re: goniometrické funkce

#7 20. 02. 2009 13:36

Re: goniometrické funkce

#8 20. 02. 2009 13:39

Re: goniometrické funkce

#9 22. 02. 2009 15:07

Re: goniometrické funkce

#10 22. 02. 2009 19:25

Re: goniometrické funkce

#11 22. 02. 2009 20:43

Re: goniometrické funkce

#12 22. 02. 2009 20:53

Re: goniometrické funkce

#13 22. 02. 2009 20:59

Re: goniometrické funkce

#14 22. 02. 2009 21:23

Re: goniometrické funkce

#15 22. 02. 2009 21:26

Re: goniometrické funkce

#16 22. 02. 2009 21:29

Re: goniometrické funkce

#17 22. 02. 2009 21:31

Re: goniometrické funkce

#18 22. 02. 2009 21:33

Re: goniometrické funkce

#19 22. 02. 2009 21:36 — Editoval jendula11 (22. 02. 2009 21:40)

Re: goniometrické funkce

#20 22. 02. 2009 21:41

Re: goniometrické funkce

#21 22. 02. 2009 21:44

Re: goniometrické funkce

#22 22. 02. 2009 21:47

Re: goniometrické funkce

#23 22. 02. 2009 21:48

Re: goniometrické funkce

Zápatí