Matematické Fórum

Janisek · 14. 09. 2014 20:34

Ahoj, potřeboval bych pomoct s kvadratickou rovnicí $px\cdot (3x+4)=x^{2}+1$ s parametrem $p$
Ověřil jsem si podmínku pro kvadratickou rovnici $p=0 \Rightarrow 0=x^{2}+1 \Rightarrow K=\emptyset$
A dál netuším, jak se pohnout, protože pokud rovnici roznásobím a upravím, nedostanu, aby byly $x^{2}$ u sebe a já mohl řešit kvadratickou rovnici..
Pomůžete mi prosím?

duskin · 14. 09. 2014 20:44

Uprav si to nejdřív celé na základní tvar $ax^2+bx+c=0$ . Pak pro různé hodnoty parametrů budou vycházet různé hodnoty v diskriminantu atd...

misaH · 14. 09. 2014 20:48 — Editoval misaH (14. 09. 2014 20:56)

↑ Janisek:

$3px^2+4px-x^2-1=0$

$(3p-1) x^2+4px-1=0$

$x_{1,2}=\frac {-4p\pm\sqrt {16p^2+4 (3p-1)\cdot 1}} {2 (3p-1)}$

Janisek · 14. 09. 2014 20:57

↑ misaH:
Tuto možnost úpravy jsem v tom vůbec neviděl, děkuju, budu pokračovat dál.. :)
↑ duskin:
Ano, už vím, jak na to..

pietro · 14. 09. 2014 21:12

Ahoj :-)

A keby bolo niekedy ťažko, aj toto sa dá opatrne použiť.

Kontrolní otázka :
Ve kterém českém filmu zazněla věta: "I dělník ve šroubárně může číst Vergilia v originále!"

Janisek · 14. 09. 2014 21:14

Takže tedy konečné řešení je:
pokud $p=0$ pak $K=\emptyset$
pokud $p=\frac{1}{3}$ pak $K=\emptyset$
pokud $R\setminus \{0;\frac{1}{3}\}$ pak $K=\frac{-4p\pm \sqrt{16p^{2}+12p+4}}{2\cdot (3p-1)}$ ?

Janisek · 14. 09. 2014 21:16

↑ pietro:
Marečku, podejte mi pero!

misaH · 14. 09. 2014 21:27

↑ Janisek:

Uvažoval si, źe ak by pod odmocninou bolo záporné číslo, rovnica by nemala riešenie?

A podobne 0 pod odmocninou dvojnásobný koreň.

zdenek1 · 14. 09. 2014 22:35

↑ Janisek:
A ještě jeden postřeh: variantu 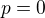$p=0$ vůbec nemusíš samostatně uvádět, ta by se ti měla automaticky objevit při rozboru diskriminantu.

Jo, a kolik je $4\cdot(-1)$ ?

Rumburak

↑ Janisek:

Ahoj.

Doporučuji pozorně si přečíst originál zadání. Je v něm výslovně uvedeno, že rovnice

$px\cdot (3x+4)=x^{2}+1$

je kvadratická ? Pokud ne, pak je potřeba připustit i případ $p = \frac{1}{3}$ , kdy jde o lineární rovnici.

Matematické Fórum

#1 14. 09. 2014 20:34

Kvadratická rovnice s parametrem

#2 14. 09. 2014 20:44

Re: Kvadratická rovnice s parametrem

#3 14. 09. 2014 20:48 — Editoval misaH (14. 09. 2014 20:56)

Re: Kvadratická rovnice s parametrem

#4 14. 09. 2014 20:57

Re: Kvadratická rovnice s parametrem

#5 14. 09. 2014 21:12

Re: Kvadratická rovnice s parametrem

#6 14. 09. 2014 21:14

Re: Kvadratická rovnice s parametrem

#7 14. 09. 2014 21:16

Re: Kvadratická rovnice s parametrem

#8 14. 09. 2014 21:27

Re: Kvadratická rovnice s parametrem

#9 14. 09. 2014 22:35

Re: Kvadratická rovnice s parametrem

#10 15. 09. 2014 10:56 — Editoval Rumburak (15. 09. 2014 10:59)

Re: Kvadratická rovnice s parametrem

Zápatí