Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 09. 2014 18:21 — Editoval <h1>dydy</h1> (16. 09. 2014 18:23)
- <h1>dydy</h1>
- Příspěvky: 155
- Reputace: 0
Reziduum víceznačné funkce
Ahoj, dostal jsem se do problému při integrování víceznačné funkce.
Integrace: Reálná kladná osa tam a zpátky, malá a velká kružnice se středem 0. Kružnice dají obě nulu.
Teď to začne být těžší: integrály po reálné ose dají hodnotu počítaného integrálu I v prvním případě, v druhém případě -I, ale jede se v protisměru, takže se znaménka vyruší a vyjde  v závislosti na výběru branche.
v závislosti na výběru branche.
Teď jádro problému:  , což je
, což je  . Ale problém, odmocnina je
. Ale problém, odmocnina je 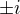 . Kterou hodnotu vzít? Je výsledek víceznačný? Kde se stala chyba? Je potřeba brát reziduum v souvislosti s s výběrem branche předtím? Podle jakého postupu?
. Kterou hodnotu vzít? Je výsledek víceznačný? Kde se stala chyba? Je potřeba brát reziduum v souvislosti s s výběrem branche předtím? Podle jakého postupu?
Výsledek v kopáčkovi je kladné pí.
PS: chtěl bych se ujistit, jaká je podmínka pro velkou kružnici: zde se píše, že stačí klesání lepší rychlejší než 1/R , což je splněno, klesá to jako R^-1.5. Zda stačí jen určit, zda to klesá jako nějaká mocnina R, nebo je nutné pečlivě hledat maximum funkce při konstantním R vůči danému úhlu bodu?
A skutečně platí, že stačí klesání jako 1/R? Na škole jsme si definovali, že stačí jako 1/R^2 (ano, je to inkluzivní vím)
Offline
#2 17. 09. 2014 11:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reziduum víceznačné funkce
Zdravím,
jen takové upřesňující dotaz - konkrétně tato úloha  je určena k použití metody, jak popisuješ (
je určena k použití metody, jak popisuješ (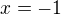 a
a  zda vůbec splňuji podmínky, že jsou singulární body vzhledem k def. oboru) a zda jsou všechny předpoklady pro použití odkazované metody?
zda vůbec splňuji podmínky, že jsou singulární body vzhledem k def. oboru) a zda jsou všechny předpoklady pro použití odkazované metody?
Není schůdnější stanovovat nevlastní integrál  (použit substituci
(použit substituci 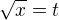 atd.) bez uvedené metody? Děkuji.
atd.) bez uvedené metody? Děkuji.
Offline
#3 17. 09. 2014 14:02
- <h1>dydy</h1>
- Příspěvky: 155
- Reputace: 0
Re: Reziduum víceznačné funkce
No byl to příklad na procvičení na komplexní analýzu, takže jsem ani jiný postup nezkoujmal (což je možná škoda se nad tím nezamyslet a porovnat to. Ano, předpoklady jsem kontroloval, mě jde čistě jen o ten problém s víceznačností, Jak jsem se dočetl v kopáčkovi v příkladu který se týkal právě této priblematiky, tak se potvrdilo, že volba správného znamínka (nebo obecně jiné hodnoty) daného rezidua záleží na definici té funkce. Zkusám sem na to dát příklad do nového vlákna až se vrátím. Na něm to všechno bude vidět.
Offline
#4 17. 09. 2014 21:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reziduum víceznačné funkce
↑ <h1>dydy</h1>:
děkuji, můj popis v ↑ příspěvku 2: je bez přechodu k komplexnímu oboru (můžeš porovnat, měl by dávat i jen v R stejný výsledek). Pokud jsem stáhla (z nejmenovaných zdrojů) správného Kopáčka, tak Tvůj problém přímo rozebírá ve větě 17.26 a v příkladu také 17.26.
Zkusám sem na to dát příklad do nového vlákna až se vrátím. Na něm to všechno bude vidět.
to bude určitě přehlednější, snad by pomohl i přímo náhled na původní text, který diskutuješ, přece jen Tvůj popis "cesty tam a zase zpátky" - no uznej :-) Zdárné pokračování s kolegy přeji.
Offline
#5 18. 09. 2014 15:22 — Editoval <h1>dydy</h1> (18. 09. 2014 15:24)
- <h1>dydy</h1>
- Příspěvky: 155
- Reputace: 0
Re: Reziduum víceznačné funkce
úprava: sakra, měl jsem rozepsáno, dal jsem tlačítko zpět a potom vpřed a text se změnil v nějakou starší verzi
Upřesnění integrační cesty: (použije se limita r->0 a R-> nekonečno)
1: 
2: 
3. 1: 
4: 
Vtip je v tom, že i když cesty 1 a 3 jsou identické, tak díky tomu, že integrand bude mít jinou hodnotu (bude vynásoben -1) nevyruší se.
Zde je obrázek odmocniny
Jsou 2 možnosti: (***)
-začne se integrovat horní větvi (0, červená (pozn: červená: odstín 0 stupnňů arg=0, tedy kladné reálné číslo), žlutá zelená azurová (180 - > e^i pi) záporné), do nuly a kružnice zpět)
-začne se spodní větví: 0, azurová modrá fialová, červená, 0 a kružnice zpět.
Výsledkem je, že buď vyjde 2* hledaný integrál "I" a nebo -2* I. Ano, I vyjde v obou případech stejně,což se rovná 2/2* pi i * residuum. Jenže residuum je 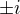 ., ale nechápu kterou větev při výpočtu residua vybrat. Protože přece při výpočtu residua žádná křivka neexistuje. A nebo je to nějak skryté a já to nevidí. Tedy nevím, jak (podle jakého pravidla)propojit vybranou cestu při integraci (viz ***) a větev při výpočtu rezidua.
., ale nechápu kterou větev při výpočtu residua vybrat. Protože přece při výpočtu residua žádná křivka neexistuje. A nebo je to nějak skryté a já to nevidí. Tedy nevím, jak (podle jakého pravidla)propojit vybranou cestu při integraci (viz ***) a větev při výpočtu rezidua.
Offline
#6 19. 09. 2014 00:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Reziduum víceznačné funkce
↑ <h1>dydy</h1>:
děkuji, pro upřesnění - komplexní analýzu znám jen v úplných základech (teoretické předpoklady pro elektrotechniku), cca v takovém rozsahu. Jak se dívám do Kopáčka (IV. díl), tak konkrétně tento typ integrálu rozebírá minimálně na 6 stránkách - zkoušel jsi projít?
Mělo by se podařit převést pomocí úprav formu ![kopírovat do textarea $\int\limits_{0}^{\infty}x^{\alpha-1} f(x)\d x =\frac{2\pi i}{1-e^{2 i \pi a}}\sum_{k=1}^{n}\mathop{\mbox{res}}\limits_{z=a_k}\left[ z^{\alpha-1} f(z)\right]$](/mathtex/4b/4b8548683aa0bf4c265a30420ce8bd0f.gif)
na ![kopírovat do textarea $\int\limits_{0}^{\infty}x^{\alpha-1} f(x)\d x =\frac{\pi}{\sin (a\pi)}\sum_{k=1}^{n}\mathop{\mbox{res}}\limits_{z=a_k}\left[ (-z)^{\alpha-1} f(z)\right]$](/mathtex/2d/2d2bbc668268c6e12ee929b612e7df11.gif)
Doufej, že se zapojí někdo z kolegů (nebo ještě jednou projdi ten studijní text). Omlouvám se, že k tématu toho moc neřeknu.
Offline
#7 19. 09. 2014 01:09
- <h1>dydy</h1>
- Příspěvky: 155
- Reputace: 0
Re: Reziduum víceznačné funkce
Ty skripta jsou dobrý, akorát mám pocit, že vyložené látka skončila uprostřed Laurentových řad. A uplně tam chybí Jordanovo lemma, velká a malá půlkružnice, integrace přes více značné funkce a typové příklady integrálů a k nim vhodné integrační křivky.
Offline
#8 19. 09. 2014 13:19 — Editoval OiBobik (19. 09. 2014 13:39)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Reziduum víceznačné funkce
↑ <h1>dydy</h1>:
Ahoj,
nečetl jsem tu otázku příliš poctivě, ale tak zkusím sem napsat, v čem si myslím, že je problém, třeba se trefím.
Reziduum funkce v nějakém bodě je definováno jako  -tý člen rozvoje dané meromorfní funkce do Laurentovy řady v uvažovaném bodě. Na tom nemůže být nic příliš nejednoznačného, pokud víš, jakou meromorfní funkci uvažuješ. Jde tedy o to, dobře rozšířit reálnou funkci
-tý člen rozvoje dané meromorfní funkce do Laurentovy řady v uvažovaném bodě. Na tom nemůže být nic příliš nejednoznačného, pokud víš, jakou meromorfní funkci uvažuješ. Jde tedy o to, dobře rozšířit reálnou funkci  na dostatečně velkou oblast v
na dostatečně velkou oblast v  .
.
Kde se tam bere nějaká zdánlivá nejednoznačnost, je, že něco jako formální předpis  definuje dvě různé funkce v závislosti na tom, kterou větev odmocniny zvolíš. V tom ale nemáš žádnou volnost: Musíš ji zvolit tak, aby při restrikci na interval
definuje dvě různé funkce v závislosti na tom, kterou větev odmocniny zvolíš. V tom ale nemáš žádnou volnost: Musíš ji zvolit tak, aby při restrikci na interval 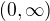 ti to dalo tvoji zkoumanou integrovanou reálnou funkci - ta druhá větev tam pravděpoobně vyprodukuje
ti to dalo tvoji zkoumanou integrovanou reálnou funkci - ta druhá větev tam pravděpoobně vyprodukuje  . Z tohoto pohledu není divu, že ti to reziduum vypadne přesně opačný, v důsledku čehož vyjde celý ten integrál přesně opačně.
. Z tohoto pohledu není divu, že ti to reziduum vypadne přesně opačný, v důsledku čehož vyjde celý ten integrál přesně opačně.
Jo a ještě dodatek:
Takhle to zní výhružně, že člověk musí projít všechno poctivě a sledovat, jestli volí tuhle správnou odmocninu a tamhle správný reziduum (a přitom celou dobu honit nějaké znaménko), ale jakmile si člověk uvědomí "co se tam děje", že ty dvě honoty rezidua přísluší těmto dvěma integrálům (tj.  a
a  ), může s docela klidným svědomím zvolit jako to "správné" reziduum to, které dává kladnou hodnotu integrálu - ač se to dělá s komplexkou, stále se v podstatě jen integruje nezáporná reálná funkce, takže výsledek nemůže být záporný...
), může s docela klidným svědomím zvolit jako to "správné" reziduum to, které dává kladnou hodnotu integrálu - ač se to dělá s komplexkou, stále se v podstatě jen integruje nezáporná reálná funkce, takže výsledek nemůže být záporný...
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline